Методичні вказівки до практичних занять з дисципліни “Оcнови теорїї захисту інформації”, страница 4

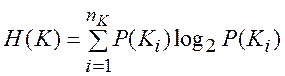
Апостеріорна ентропія  визначається через умовну апостеріорну імовірність .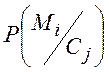

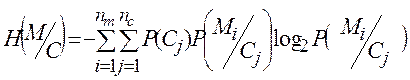                                          (1.12)

 можна розрахувати за (1.12), знаючи статистику Р(С_j) і знаючи статистику .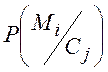

Під надмірністю d розуміється міра корельованості (залежності) символів у мові і нерівноймовірної їх появи в повідомленні.

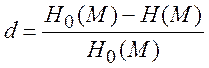
Н₀(М) – ентропія мови, де всі символи рівно ймовірні і незалежні.

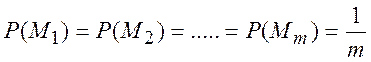
Для цієї умови

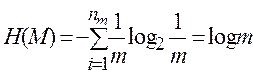=Н₀                                                                            (1.13)

Якщо  то

                                                   (1.14)

Розв’язавши (1.14) маємо

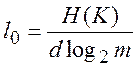
При m = 2 маємо

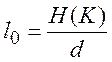  (якщо m=2)                                               (1.15)

Симетричні шифри являють собою безліч функцій  криптографічних перетворень (або відображень) повідомлень М в криптограми С згідно із значенням ключа К (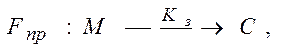) і функції зворотного перетворення: відображає безліч криптограм на безліч повідомлень згідно із законом ключа розшифрування ().

Усі симетричні шифри розділяються на блокові, потокові, складові.

Прикладом блокового шифру, є шифр підстановки безліч повідомлень посимвольно відображається само в себе згідно із законом ключа.

Кожній букві початкового алфавіту ставиться у відповідність буква перетвореного алфавіту.

1.3 Приклади розв’язку задач

Задача 1

Зашифрувати повідомлення «Пароль ХТМОРУ СЛАВА» методом простої підстановки, алфавіт російський. Визначити розмірність простору ключів n_k, ентропію H(k), безпечний час t_б та відстань єдності l₀, якщо потужність криптоаналітичної системи вар/с. Розшифрувати повідомлення і пересвідчитися в однозначності процедури зашифрування.

Ключ:

Вх:

а

б

в

г

д

е

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

Вих:

ж

и

к

м

о

р

т

у

х

ч

щ

ы

э

я

а

б

в

г

д

е

з

й

л

н

п

с

ю

Розв’язок задачі:

Використовуючи ключ підстановки зашифруємо повідомлення «Пароль ХТМОРУ СЛАВА» . Зашифроване повідомлення має вигляд:

С = «бжваыцюйдэавеюгыжкж»

Знаходимо розмір простору ключів:

N_кл = m! = 32! = 2,6 *10³⁵ » 2¹¹⁷

де

m - основа алфавіту.

Знаходимо ентропію джерела ключів:

H(k) =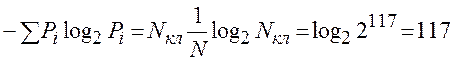

Далі визначаємо безпечний час:

t_б =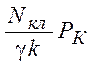

де P_K є  імовірність з якою повинен бути здійснений критоаналіз

В результаті маємо:

t_б = 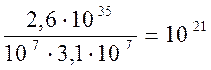років

Таким чином може володіти дуже високою стійкістю, але у зв'язку з тим, що природні мови володіють значною надмірністю пов'язаною з нерівнорівномірністю появи букв в мові і залежністю букв між собою, існує ефективний метод частотного криптоаналіза. Суть аналізу: набирається об'єм не менше за 2000 символів, далі будується гістограма частот появи символів в криптограмі.

Відстань єдності для шифру:

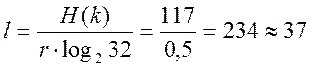літер

Задача 2.

Зашифрувати повідомлення (див. задача 1) використовуючи шифр Віжінера.

Ключ: “Ну погоди”. Тобто ключ має довжину 9 символів.

Розв’язок задачі:

Проаналізуємо букви алфавіту, згідно таблиці

а	Б	в	Г	д	е	ж	з	И	й	к	л	м	н	о	п	р
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
с	Т	у	Ф	х	ц	ч	ш	щ	ы	ь	э	ю	я
17	18	19	20	21	22	23	24	25	26	27	28	29	30