Идентификация объектов и систем. Модели, типы моделей и их использование. Типы идентифицируемых объектов. Характеристики случайных процессов и случайных величин. Требования, предъявляемые к методам идентификации, страница 9

Q(ε)=ε²(t) – приходит к критерию средней квадратичной ошибки, применение которого приводит к простым алгоритмам идентификации.

3) Q(ε)=ε(t)

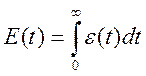 - равномерный критерий.

Недостатком, которого является то, что минимум может достигаться не только в точках наибольшей близости у и у_m. Но также и в тех точках, где положительные и отрицательные отклонения приблизительно равны. Этого недостатка можно избежать, если взять модель ε(t), т.е.

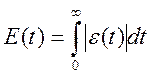
Недостаток оценки: указанный интеграл, оказывается, найти затруднительно. Критерий адекватности могут быть улучшены за счет рационального выбора функций w(t).

Считается удачный выбор функции:       

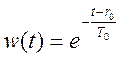
Т₀ – наперед заданное времени памяти.

В ряде случаев используют критерии, учитывающий входной сигнал:

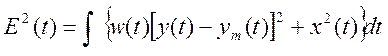
В общем случае могут быть использованы также и другие критерии адекватности, причем выбор подходящего критерия адекватности представляет собой в ряде случаев не простую задачу и диктуется во многом особенностями решаемой задачи идентификации. А также уровнем мастерства исследования.

Точность идентификации

При решении задачи идентификации следует стремиться к тому, чтобы производный над объектом эксперимент, обеспечивая максимум полезной информации при минимальном количестве и продолжительности опытов.

В общем случае оценка параметров объекта по результатам эксперимента носит приблизительный характер. Погрешности оценок могут быть обусловлены целым рядом фактором: не индивидуальностью принятой моделью, наличием шага квантования сигнала, ограниченностью времени наблюдений и т.д.

Перечисленные факторы в их направленном единстве, поскольку они могут влиять друг на друга.

Рассмотрим некоторые виды возникающих погрешностей:

1.  Оценки, связанные с наличием шумов.

Присутствие шумов при проведении измерений на технических объектах не только мешает получению достоверных данных, но в ряде случаев делает это даже невозможным. В качестве шумов при проведении механических испытаний могут наступать случайные вибрационные возможности.

При электрических измерениях могут сказываться помехи в электрических деталях.

В этих случаях для получения количественных оценок приходится вводить косвенные показатели; например: сигнал/шум.

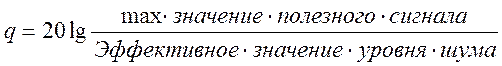
Данное выражение имеет смысл для широкополосных шумов. Если в процессе идентификации параметр q оказывается малым, то следует использовать различные методы увеличения этого параметра. Как показали исследования, обработка результатов измерения переходной характеристики возможно, если q>16dB. А для импульсной переходной характеристики Q>6dB.

К числу простейших способов улучшения этого параметра относится фильтрация ВЧ (высоко частотных) сигналов и сглаживания экспериментальных данных. Другим эффективным способом повышения q является многократное повторение измерений с последующим усреднением. Известно, что среднее квадратное отклонение стационарной помехи после n измерений:

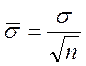
- средняя квадратичная ошибка измерений.

Повышение параметра q:  ∆q=10 lg n

Эффективным средством повышения малых неустойчивости процесса идентификации является применение моделей и сравнение выходных координат с соответствующей координатами объекта в смысле некоторого критерия близости.

При решении таких задач приходится, как правило, перебирать несколько вариантов аппроксимации экспериментальных данных.

Такая аппроксимация может быть достигнута путем использования экспериментальной функции степенных, тригонометрических компонентов и т.д.

2. Ошибки за счет не идеальности модели. Эти ошибки могут быть связаны с конечной длительностью переходных процессов, конечной полосой пропускания, нестабильностью характеристики объекта. Например: продолжительностью наблюдения за объектом должна быть такой, чтобы переходный процесс успел завершиться до подачи следующего типового воздействия.

При конечной полосе пропускания системы динамические характеристики объекта без существенных потерь точности могут быть представлены в виде ряда дискретных значений, причем интервал дискретизации.

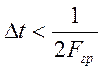
в соответствии с теоремой Котельникова, должен выбираться из предыдущего условия.