Идентификация моделей таких временных рядов производится итерационными методами, причем модели этих рядов бывают трех видов:
1. Авторерессионные модели
2. Модели авторегрессии со скользящим значением.
3. Авторегрессионые с проинтегрированным средним значением.
На основании соответствующих методик по указанным моделям может получена с достаточно высокой степенью точности прогнозирования развитие процесса.
Характерной особенностью авторегрессионных моделей временных рядов является то, что чем выше порядок модели, тем больше число членов временного ряда необходимо учитывать при прогнозировании и тем более сложной является их математическая зависимость.
Методы идентификации моделей временных рядов в последнее время интенсивно развивается, находит широкое применение в связи с интенсивным использованием ЭВМ.
Интерполяция с помощью сплайн – функции.
Данная интерполяция наиболее эффективна для построения гладких кривых, проходящих через заданные точки, полученные например, экспериментально.
Если имеется некоторое число n – точек, то при сплайне интерполяции через каждые две соседние точки проводят поленом третей степени.
Понятно, что по этим двум точкам нельзя однозначно определить коэффициенты этого полинома, поскольку две точки определяют только полином первой степени, т.е. прямую.
Для некоторого i-го полинома 
, проходящего через точки 
можно записать следующую систему:
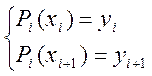
Причем переход от полинома 
должен быть плавным.
Для выполнения этих условий значение
первой и второй производных для соседних полиномов в их общей точке 
, т.е. должны выполняться:
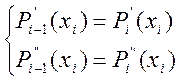
Таким образом, для внутренних полиномов сформулировано четыре условия, которые достаточны для их построения.
Обе концевые точки исходного массива имеют только по одной соседней, поэтому для построения концевых полиномов требуются дополнительные условия.
Если принять, что точки, лежащие в не рассматриваемом интервале, можно аппроксимировать, то последнее условие можно записать в виде:
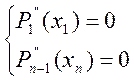
На основании решения полученной системы, выполненной
по определенной методике, можно полностью определить сплайн полиномы .
А тогда для любого значения 
можно
рассчитать интерполяционное значение .
В настоящее время для реализации сплайн интерполяции существуют стандартные программы для ЭВМ.
Данный метод очень удобен с точки зрения представления гладких зависимостей, при условии, что наш изначально известно, что процесс является непрерывным и не имеет точек разрыва.
Регрессионная зависимость на основе сплайн используется для сглаживания экспериментальных данных и их более наглядного представления, причем степень сглаживания может задаваться самим исследователем.
При такой интерполяции сплайн функции проходят через все экспериментальные точки, причем эти точки совпадают с точками перегиба сплайн функции.
Если уменьшить число точек перегиба, то сплайн функция не будет точно проходить через экспериментальные точки.
Поэтому дополнительные условия для построения такой сплайн функции заключается в том, чтобы сумма квадратов отклонений заданных точек от аппроксимирующих функций была минимальна, т.е. точки должны располагаться на одинаковом расстоянии от соответствующих кривых.
Чем меньше число точек перегиба, тем более гладкой получится кривая, тем дальше будет проходить в стороне от заданных точек.
Вопросы самоконтроля:
1. Виды идентифицирующих моделей с использованием временных рядов?
2. В чем заключается особенность авторегрессионных моделей временных рядов?
3. Для чего используется интерполяция с помощью сплайн – функции?
Идентификация моделей процессов методом планирования экспериментов
(Изучено самостоятельно).
Лекция №13
Цель лекции: изучение основных понятий технической диагностики систем
Техническая диагностика систем
Важной и актуальной проблемой является проблема обеспечения качества и надежности функционирования сложных технических систем.
Распознавание технического состояния объекта на важных этапах его жизненного цикла представляет собой задачу технического диагностирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.