Идентификация объектов и систем. Модели, типы моделей и их использование. Типы идентифицируемых объектов. Характеристики случайных процессов и случайных величин. Требования, предъявляемые к методам идентификации, страница 15

Цель лекции: изучение методов идентификации, основанных на аппроксимирующих характеристиках  объектов.

Методы идентификации, основанные на аппроксимирующих характеристиках объектов

В связи с большими погрешностями решение уравнения Винера-Хопфа возникающие при использовании нестандартных сигналов. Предложены специальные методы построения этого решения с использованием некоторых функционалов.

В качестве решения могут быть использованы, так называемые, гладкие решения, получение которых основано на том, что динамические характеристики объектов апроксимируется некоторыми функциями, при этом коэффициенты в этих функциональных выражениях получаются путем обработки входных и выходных сигналов.

При этом точность аппроксимации определяется путем использования критерия близости объекта и модели, которые задаются функционалом ошибки.

При этом задача идентификации распадается на две составляющие:

1. Выбор вида аппроксимирующих функций.

2. Подбор параметров этих функций, причем стараются получить желаемую точность, при как можно меньшем числе используемых функций.

Данный метод базируется на аппроксимации импульсных передаточных функций АКФ, функции обладают тем преимуществом, что позволяет получить достаточно простые алгоритмы идентификации, в том числе и адаптивные.

Метод аппроксимации в теоретическом плане основан на том, что, согласно теоремам математического анализа, любая абсолютно интегрированная на интервале [0, Т] функция f(t), может быть разложена по некоторой системе аппроксимирующих функций.

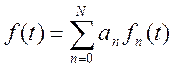
При этом функции  должны быть интегрируемы, должны быть достаточно легко реализуемы на ЭВМ.

В качестве такой системы функции могут быть использованы тригонометрические функции, а так же целый ряд специальных полиномов.

Если в процессе идентификации регистрируется импульсная передаточная функция , то наиболее часто она апроксимируется полиномами Логгера вида:

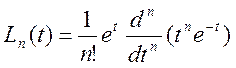
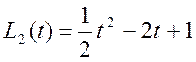   и т.д.

При этом на практике число использованных полиномов обычно не превышает .

В некоторых случаях экспериментально регистрируется АКФ и ВКФ, допускающих аппроксимацию полиномов Логгера и Чебышева.

Для этих случаев разработан метод типовой идентификации, основанный на том, что с учетом накопленного опыта и теоретических исследований на базе наиболее часто встречающихся входных и выходных сигналов выбирают оператор близких и истинному оператору объекта.

Наличие специальных таблиц типовых идентификаций позволяет определить АКФ и ВКФ в аналитическом виде. Затем из таблиц найти подходящий оператор (в виде диффиринциальных уравнений), а затем определить параметры и другие характеристики модели на основе экспериментальных значений.

В качестве типовых входных воздействий наиболее часто используются импульсные воздействия АВФ, который имеет вид:

1)  

2)

3)

Рассмотренный метод послужит основой для построения альбомов или атласов типовой идентификации линейных объектов, где а таблицах для наиболее характерных АВК и ВКФ приводятся соответствующие выражения для импульсных передаточных функций, что упрощает и ускорят процедуры идентификации типовых объектов.

Вопросы самоконтроля:

1. Как определяется точность аппроксимации?

2. Какие ставятся задачи идентификации?

3. В чем преимущества данного метода аппроксимации?

4. На чем основан  метод аппроксимации?

Лекция № 10.

Цель лекции: изучение специальных методов идентификации .

Идентификация с помощью адаптивных моделей

Смысл адаптивных моделей заключаются в том, что такие модели позволяют оперативно подстраивать параметры модели под характеристиками объекта.

Адаптивная модель может представлять аппаратный либо алгоритмический комплекс, который можно изобразить.  

 

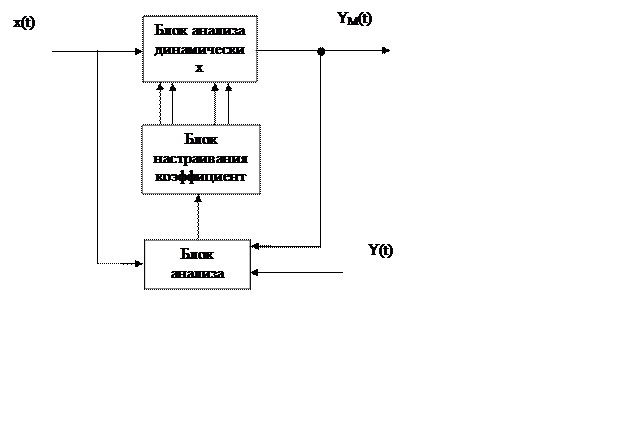Блок динамических характеристик  фактически является собственно моделью объекта представленной, на пример, системой,  некоторых  ортогональных функций, по которым разложена импульсная передаточная функция.

Блок настраивания коэффициентов - служит для установки коэффициентов модели путем подбора которых достигается требуемая близость выходных координат объекта Y(t) и модели Yм(t).