Адаптивные модели обусловлены недостатком априорной информации об объекте управления. Адаптивный подход предполагает текущее определение характеристик исследуемого процесса при нормальном его протекании. А получаемые оценки используются для улучшения модели объекта.
Все сказанное позволяет классифицировать методы идентификации в зависимости от принятой математической модели вида входных воздействий, принимаемых средств вычислительной техники.
Математическое описание исследуемого объекта можно получать в различном виде. При этом характеристики модели должны как можно лучше соответствовать характеристикам объекта.
Выбор модели реального объекта должен осуществляться с учетом требуемой точности соответствия моделей реального объекта.
Наиболее полно разработаны методы идентификации линейных объектов в качестве математического описания таких объектов, используются непараметрическое и параметрическое описания исследуемых процессов.
В этом случае наиболее универсальным является не в параметрическом представлении на основе использования функциональных рядов Вольтера. Однако в ряде случаев приходится или является достаточным ограничится конечным числом членом такого ряда. Это позволяет в ряде случаев получить параметрическое описание исследуемыми процессов.
Один и тот же исследуемый объект может быть адекватно предоставлен различными видами математических моделей.
а) с помощью коэффициентов диффиринцированного уравнения или весовой функции;
б) амплитудной или фазочастотной характеристикой;
в) путем аппроксимации динамических характеристик объекта, некоторой системы функций, допускающей подстройку доминирующих параметров.
Любая динамическая система вполне определенного образа
преобразует входной сигнал 
в входной сигнал 
.
 |
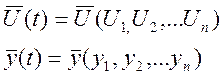
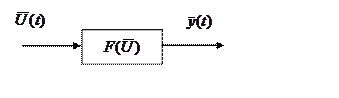(1)
Соотношение (1) характеризует правило преобразования
вектора 
. Величина F – оператор
модуля.
Явный вид оператора F, как правило, требуется в процессе идентификации. В частности в качестве оператора F, в ряде случаев, может выступать передаточная функция W(P).
Изобразим общую схему задачи идентификации в следующем виде:
 |
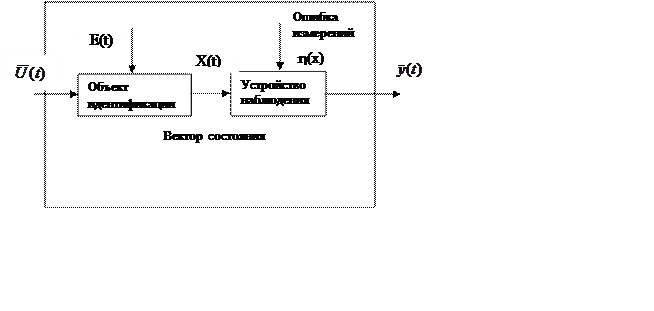- (2) уравнение
наблюдения объекта идентификации.
В общем случае величины 
и 
содержат в себе статические компоненты.
Таким образом, соотношение (2) Вт общем случае является стохастическим. Однако
при условии 
то соотношение (1) в общем случае
идентификации объекта почти целиком определяется соотношением двух факторов.
- объем априорной информации о структуре объекта,
- объем измеренной информации.
Изначально априорные сведения об объекте позволяют в определенной степени определить структуру объекта: число входов и выходов, характер связи на основе имеющей информации.
На основании измерительной информации, полученной в результате проведения эксперимента над объектом, могут быть получены значения интересующих параметров моделей объектов. В этом случае достигается осуществление параметрической идентификации.
Специфика решения задач идентификации главным образом связана со степенью наблюдаемости входного сигнала, который может быть, наблюдаем точно и соблюдаем сочетание смысла шумов или не наблюдаем.
В любом случае содержит
искажения, обусловленное погрешностью измерения.
Методы идентификации
Методы идентификации можно классифицировать путем деления на 8 следующих групп:
1) Объекты, в зависимости от степени предварительной изученности объекта. По наличию априорной информации объекты могут быть разделены на 4 вида:
- объекты, для которых уравнение, описывающее поведение является известным вплоть до приближенных значений коэффициентов.
- объекты, которых известно уравнение, но не известно значение коэффициентов этих уравнений (общий вид).
- объекты, для которых конкретный вид уравнений не известен, но известна некоторая предварительная информация по характеристикам объекта.
- объекты, относительно которых полностью отсутствует предварительная априорная информация (объекты типа черного ящика).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.