Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно в практическом применении, поэтому в качестве показателя рассеивания используется арифметическое значение квадратного корня из дисперсии, то есть средне квадратичное отклонение:
![]()
Для непрерывной случайной величины дисперсия находится по следующей формуле:
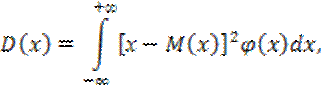
где ![]() – функция распределения
– функция распределения
Оценка среднеквадратичного отклонения определятся по формуле:
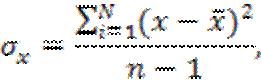
где (n-1) - степень свободы
Автокорреляционная функция
Случайные величины x1(t), x2(t) отличатся скоростью изменения во времени. Данные сигналы имеют различные спектральные составляющие, то есть высокочастотные и низкочастотные компоненты. Скорость изменения случайной величины во времени характеризуется автокорреляционной функцией:
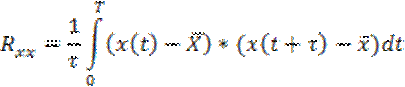
Вид автокорреляционной функции и время ее затухания является количественной оценкой случайного процесса.
Для низкочастотных сигналов время затухания автокорреляционной функции увеличивается.
Корреляция – стахостическая связь между случайными величинами, то есть время затухания корреляционной функции, которая показывает продолжительность времени, на котором точки случайного процесса имеют между собой стахостическую связь.
Для низкочастотных сигналов продолжительность времени, на которых имеются стахостическая связь увеличивается.
Спектральная плотность
Второй оценкой скорости изменения случайной величины в спектральной области (частотной области) является спектральная плотность.
Спектральная плотность показывает разложение дисперсии (мощности) по частоте, то есть случайный процесс можно разложить на гармоники. Каждая гармоника характеризуется своей частотой и своей дисперсией.
x(t)=x1(t)+x2(t)+x3(t)
![]()
![]()
![]()
График, показывающий мощность гармоник случайного
процесса и их распространение по частоте называется спектральной
плотностью ![]()
Он получен путем преобразования Фурье автокорреляционной функции:
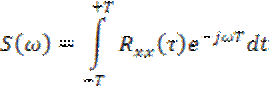
Площадь под кривой спектральной плотностью равна сумме дисперсий гармоник, то есть равна дисперсии исходного случайного процесса:
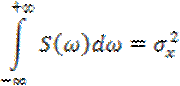
Таким образом спектральная плотность – эторазложение дисперсии случайного процесса по частотам гармонических составляющих.
Вопросы самоконтроля:
1. Что называют математическим ожиданием?
2. Что такое дисперсия?
3. Основные законы распределения случайной величины.
4. Что характеризует автокорреляционная функция?
5. Что характеризует спектральная плотность?
Лекция № 4.
Цель лекции: изучение характеристик оценки качества и идентификации.
Критерии адекватности объекта и модели
Для решения задач идентификации необходимо ввести некоторый способ оценки в области объекта и описывающей его модели.
Для этого целесообразно воспользоваться выбором некоторого критерия адекватности. На практике наиболее часто принято использовать байсовые критерии минимума среднего риска.
Обозначим у(t) – выходной сигнал объекта, уm(t) – выходной сигнал модели.
Рассогласование: ![]() .
.
Принято оценивать точность идентификации в каждом конкретном случае значением Q(ε) (функция потерь).
Значение величины ε(t) не всегда в равной степени, не во все моменты времени могут быть равноценными, с точки зрения значимости для управления. Поэтому дополнительно вводят функцию значимости: w(t) – функция веса.
Для данной реализации входной величины x(t) качество решения задачи идентификации, в среднем, принято оценивать математическое ожидание функции потерь.
![]() - средний риск.
- средний риск.
Большинство решений задач идентификации являются байсовыми, поскольку получается на основе критерия минимума среднего риска:
k(Q)→min
Вбирая тот или иной вид потерь Q(t) можно получить ряд критериев, применяемых на практике при решении тех или иных задач идентификации.
1) Пусть функция веса w(t)=1. Это означает, что значение ε(t) во все моменты времени равноценны.
Выбираем функцию потерь:
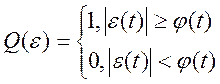
Тогда ![]() -
значение среднего риска.
-
значение среднего риска.
Это вероятность того, что рассогласование ε(t) выходит за пределы (-φ(t),φ(t)).
2) Пусть Q(ε)=c-δ(ε(t)). Используемую оценку получают критерий максимального правдоподобия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.