Недостатком детерминированных методов является слабая
или низкая помехоустойчивость, что приводит к необходимости использовать
статистический подход к определению 
ИПФ.
Стохастические методы в основном корреляционные основаны на решении уравнения:
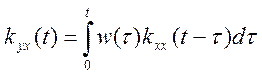- уравнение
Винера-Хопфа.
Наиболее просто ИПФ может быть найдено, если в качестве входного сигнала используется белый шум.
Поскольку АКФ такого сигнала является известной функцией.
Знание ИПФ позволяет определить передаточную функцию 
.
Рассмотренные методы идентификации относятся к тестовым методам.
В ряде случаев, когда отсутствует возможность применения тестового сигнала, поэтому приходится использовать стохастические характеристики, которые присутствуют в процессе естественного функционирования процесса.
При этом задача идентификация разбивается на два этапа:
1. Определение статических характеристик случайных процессов в объекте.
2. Построение модели объектов.
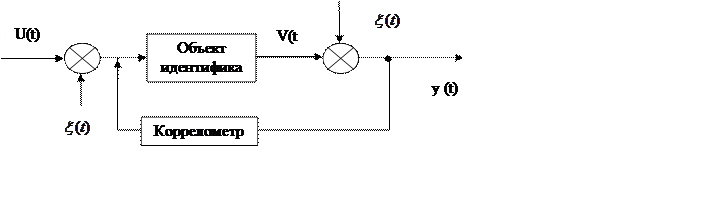
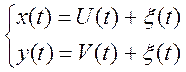
При отсутствии корреляционной связи помех с входными и выходными сигналами.
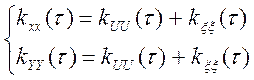
Предположим, что помехи представляют собой белый шум. Это означает:
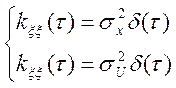
В таком случае можно записать:
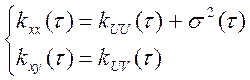
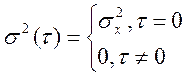
Что означает, что замена 
на 
дает ошибку только при 
.
Изложенная выше методика, основанная на применении корреляционного метода позволяет минимизировать влияние помех, причем ошибка идентификации получается тем меньше, чем больше интервал наблюдения стационарного случайного процесса.
Для идентификации импульсных придаточных функций может быть использовано уравнение вида Винера-Хопфа.
Причем наибольшая эффективность идентификации достигается, если в качестве входного сигнала используется сигнал типа белого шума.
Как правило, на практике это условие обычно выполняется поскольку в большинстве случаев можно подобрать воздействие, спектр которого значительно шире полосы пропускания динамической системы.
В этом случае, когда 
, а 
, тогда получим:
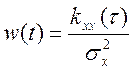
Рассмотрим применение корреляционного метода для определения передаточной функции систем, находящейся под воздействием стохастического сигнала типа белый шум.
Предположим, что зарегистрирована автокорреляционная функция выходного сигнала динамической системы второго порядка, и получено аналитическое выражение вида:
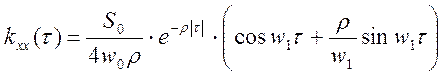
где 
- собственная частота
динамической системы.
Для вычисления передаточной функции, воспользуемся условием:
Если входной сигнал представляет собой белый шум, то
величину 
.
можно получить, если
воспользоваться соответствием:
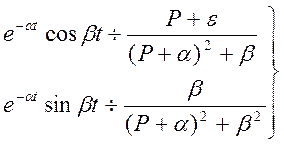
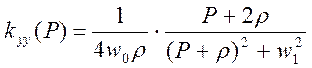(1)
(2)
Подставим (1) в (2)
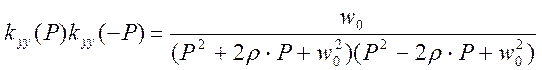
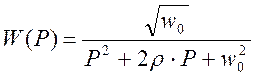
Описанная методика применима и в других случаях, когда экспериментальная АКФ апроксимируется другими аналитическими выражениями, допускающие преобразование Лапласа.
Метод идентификации динамических систем, основанный на применении корреляционного анализа имеет следующие достоинства:
1. Вычисление корреляционных функций на достаточно длительном временном интервале, позволяет снизить амплитуду ровного сигнала так, чтобы объект не испытывал существенных возмущений.
2. В ряде случаев, процессы в системе в ходе ее нормального функционирования имеют стохастический характер. Что позволяет вообще обходиться без пробных сигналов.
3. При использовании данного метода не требуется априорных знаний об объекте.
В некоторых случаях входной сигнал не может быть представлен в виде белого шума, численное интегрирование дискретного интегрального уравнения свертки в случае сигналов отличных от белого шума.
В случае сигналов, отличных от белого шума, является практичным, является представление автокорреляционной функции.
И может привести к значительным отклонениям решения задачи идентификации.
Вопросы самоконтроля:
1. Какие существуют методы определения импульсной переходной функции?
2. На какие виды подразделяются детерминированные методы определения импульсной переходной функции?
3. На чем основаны стохастические методы определения импульсной переходной функции?
4. Какие имеет достоинства метод идентификации динамических систем, основанный на применении корреляционного анализа?
Лекция № 9
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.