Общие сведения о регрессионных моделях
При проведении различных исследований различных исследований часто приходится отыскивать и изучать связи между различными процессами и их характеристиками.
Если некоторая величина 
однозначна
связана с некоторой величиной 
, то такая связь
называется функциональной, т.е. 
.
На практике между двумя случайными величинами может существовать стохастическая связь, проявляющаяся в изменении закона распределения этих величин, обнаруживать эту связь удается, как правило, только в результате многочисленных измерений и последующей статической обработки полученных результатов.
Для установления вида зависимости, при стохастической связи величины, т.е. для идентификации этой зависимости используется регрессионный анализ.
При этом различают положительную линейную и нелинейную, отрицательную и неотрицательную регрессии.
Функция регрессии определяется в виде соответствующего математического уравнения того или иного типа.
С помощью функции регрессии можно установить значение зависимой величины внутри интервала, заданные значения независимой переменной или же оценить в течении процесса внезапного интервала.
Внедрение в практику ЭВМ и разработка стандартных программ по регрессионному анализу существенно ускоряет и облегчает обработку больших массивов статических данных и дает возможность построения многократных моделей.
Под этой зависимостью понимают одностороннюю стохастическую связь.
Не известные параметры регрессии 
и 
вычисляются
с помощью наименьших квадратов по уравнению:
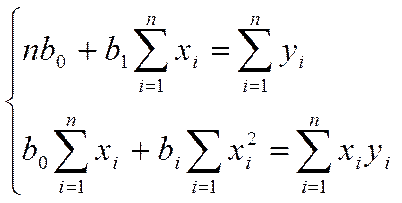
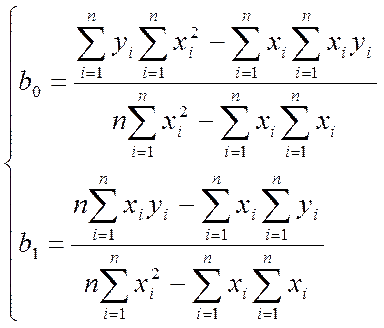
Помимо простой линейной регрессии может использоваться множественно линейная регрессия вида:
В этом случае, переменные 
оказывают
соответственное влияние на зависимую переменную .
Расчет коэффициентов множественной регрессии осуществляются по регрессии, изложенной в специальной литературе.
Нелинейная регрессия
Под нелинейной регрессией понимают более сложную одностороннюю стохастическую зависимость, представимую в виде полиноминальной модели вида:
Могут применяться также степенные, показательные, логарифмические, тригонометрические, а также полиномы Чебышева и т. д.
Обычно подбор конкретной функции осуществляется на базе той науки в рамках которой изучается данный процесс.
Принято различать два класса уравнений нелинейной регрессии:
Первый класс – охватывает регрессии нелинейные
относительно входного параметра х, но линейные относительно коэффициентов 
. Для таких регрессий применим метод
наименьших квадратов.
Второй класс – охватывает регрессии, которые являются
нелинейными также относительно коэффициентов , что
требует для применения итерационных методов.
Достаточно часто в различных технических исследованиях исследуется параболическая регрессия к-го порядка.
Для случая к=2 такая регрессия имеет вид:
В этом случае для нахождения коэффициентов составляется система трех уравнений:
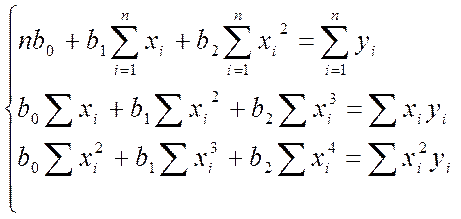
Необходимо иметь в виду, что после вычисления
коэффициента всегда должна осуществляться проверка их
значимости по соответствующей методике и незначимые коэффициенты обнуляются.
Вопросы самоконтроля:
1. Цель регрессионного анализа.
2. Виды регрессии?
1. Что понимают под нелинейной регрессией?
2. Какие существуют классы нелинейной регрессии?
3. Для какого класса регрессий применим МНК?
4. Вид уравнения параболической регрессии к-го порядка.
5. Уравнение линейной регрессии.
Лекция №12
Цель лекции: Использование временных рядов и сплайн – функции в задачах идентификации.
Использование временных рядов в задачах идентификации.
При исследовании динамики процессов в технике, а также в экономике, биологии и в других науках, важную роль играют вопросы изучения характерных признаков последовательности возникающих значений.
По результатам наблюдений строятся хронологические (временные) ряды получаемых значений.
Для таких рядов разработаны специальные методы статистической обработки, которые называются авторегрессионными, поскольку значения членов временного ряда взаимосвязаны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.