Идентификация объектов и систем. Модели, типы моделей и их использование. Типы идентифицируемых объектов. Характеристики случайных процессов и случайных величин. Требования, предъявляемые к методам идентификации, страница 13

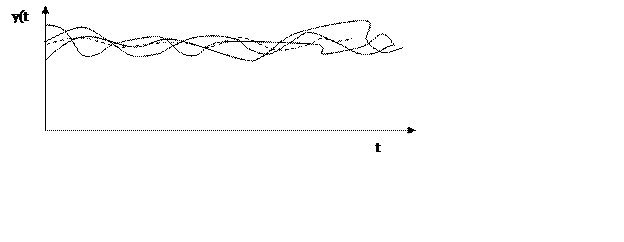
Достаточно часто при исследовании динамических характеристик технических объектов искомая переходная функция h(t) может быть искажена случайной помехой :

Так что результат наблюдения. Так как y(t) – экспериментальная функция, то определяем по ней характеристики динамической системы, возможна лишь в результате соответствующей обработки экспериментальных данных, т.е. соответствующей обработки экспериментальных данных, которая позволила бы найти истинное значение h(t).

В принципе, нахождение этой функции возможно путем усреднения функции y(t) по совокупности экспериментальных данных, при условии, что случайная функция помехи  подчиняется нормальному закону распределения.

Тогда

Для получения достоверных результатов число снятых экспериментальных функций y(t) должно быть не менее 20, что во многих случаях является критически не реальных.

 

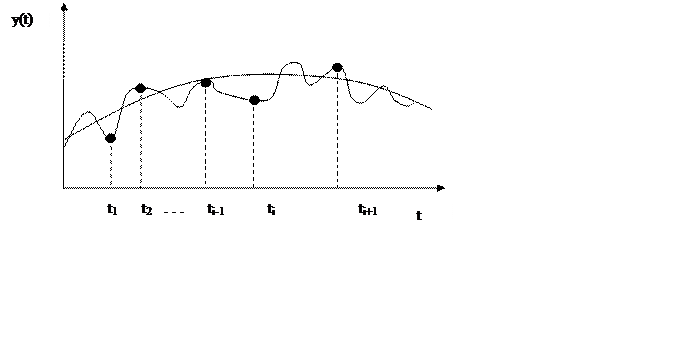
        В связи с этим, большой практический интерес представляет инженерные методы согласования и фильтрации экспериментальных кривых, заданных равно отстоящими дискретными значениями.

смежными через интервал

 

В настоящее время существует или разработано большое количество сглаженных экспериментальных функций:

- скользящей медианы,

- экспоненциальной,

- рядами Фурье,

- многочленами Чебышева.

Конкретный выбор метода определяется как характером переходной функции и требуемой точности ее определения, так и техническими возможностями инженерного персонала.

К числу наиболее распространенных методов относится метод скользящих звеньев, который применяется для апериодических переходных функций.

Суть метода заключается в последовательном усреднении ординат  на некотором интервале времени равном , где k<n и k – четное число.

Усреднение выполняется по формуле.

,           

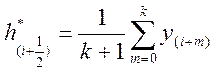 - ордината оценки переходной функции .

Интервал  - называют памятью линейного фильтра.

Фильтр такого типа обладает ограниченной полосой пропускания, что существенно снижает влияние гармонии в исходном процессе.

После выполнения операции сглаживания, экспериментальная кривая апроксимируется выражение типа.

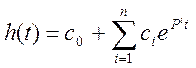
где  - установившееся значение переходного процесса,

      - неизвестные постоянные,    - корни характеристического уравнения динамической системы.

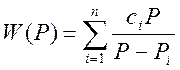
Из формулы для видно, что для ее нахождения нужно определить  значения коэффициентов  и .

С этой целью применяют специальный метод, основанный на использовании  значений экспериментальных функций.

Вопросы самоконтроля:

1. Принцип метода идентификации по переходным функциям.

2. Какие существуют сглаженные экспериментальные функции?

3. Что называют памятью линейного фильтра?

4. Чем обладает линейный фильтр?

5. Каким выражением апроксимируется  экспериментальная кривая после выполнения операции сглаживания?

Лекция № 8

Цель лекции: изучение идентификации динамических характеристик объектов по импульсным переходным функциям.

Идентификация по импульсным переходным функциям

На практике при идентификация динамических систем чаще всего используются импульсные переходные функции .

Описание объектов с помощью ИПФ имеет ряд преимуществ: минимум априорная информация об объекте, т.е. о структуре параметра, сравнительная простота перехода к другим формам описания динамических систем.

Метод определения ИПФ основан на решении уравнения типа сватки:

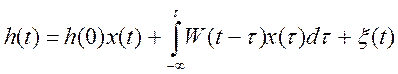
Учитывая, что для физически реализуемых объектов, то

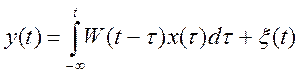
Методы определения ИПФ можно разделить на детерминированные и стохастические.

Детерминированные методы в свою очередь можно разделить на следующие виды:

1)  Метод, в котором ИНФ определяется непосредственно как реакция на .

                                                         

2) Метод, основанный на аналитическом или численном решении дискретного интегрального уравнения свертки.

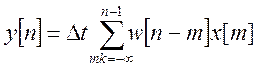
Наиболее просто ИПФ определяется на основе первого метода.

Аналитически выражение для

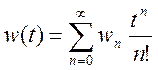
где  - определяется через дискретные значения выходного сигнала.