Идентификация объектов и систем. Модели, типы моделей и их использование. Типы идентифицируемых объектов. Характеристики случайных процессов и случайных величин. Требования, предъявляемые к методам идентификации, страница 7

4.  Какие виды существуют у детерминированных сигналов?

5.  Виды стохастических сигналов.

Лекция № 4.

Цель лекции: изучение характеристики случайных процессов и случайных величин.

Характеристики случайных процессов и случайных величин

Система управления обычно моделируется при двух видах задающих и возмущающих воздействий:

 – детерминирующих сигналов (закон которых известен и может прогнозироваться во времени);

– случайный – стахостических сигналов, зависит от большого количества факторов, точное прогнозирование которых невозможно. Но они обладают определенными закономерностями и параметрами, зная которые можно построить технологический процесс или систему управления.

1.  Математическое ожидание – М(х)

2.  Дисперсия D(x)

3.  Функция распределения F(x)

 - плотность распределения для непрерывных величин

4.  Корреляционная функция R_xx(x)

5.  Спектральная плотность

Математическое ожидание и дисперсия  - это числовые характеристики

Корреляционная функция и спектральная плотность определяют скорость изменения случайной величины.

Случайные величины бывают дискретные и непрерывные.

Случайная величина называется дискретной, если множество ее значений конечно или бесконечно, но счетно, то есть элементы можно пронумеровать натуральными числами.

Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема во всех случаях, кроме точек излома.

Функция распределения F(x) случайной величины Х называется функция выражающая для каждого текущего х вероятность того, что случайная величина Х примет значение меньше текущего значения х:

          Вероятность события – отношение количества событий благоприятствующих случайной величины к общему количеству выпадений.

          Задание непрерывной случайной величины с помощью функции распределения не является единственным способом, поэтому введем еще одно понятие для случайной величины – плотность распределения непрерывной случайной величины – это производная ее функции распределения  Она существует только для непрерывных случайных величин.

          График плотности вероятности называется кривой распределения.

Существуют различные законы распределения как для дискретных величин, так и для непрерывных случайных величин.

Основные законы распределения непрерывных случайных величин

1.  Равномерный закон распределения.

Равномерный закон на отрезке  А и В имеет плотность вероятности F(x) постоянную и вне этого отрезка равную нулю.

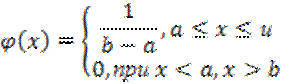
Функция распределения имеет следующий вид:

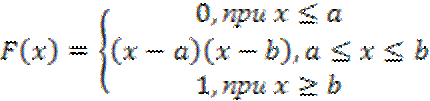
2.  Показательный закон распределения (экспоненциальный)

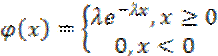
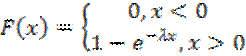
3.  Закон распределения случайной непрерывной величины (закон Гаусса)

С параметром a и  имеет плотность вероятности:

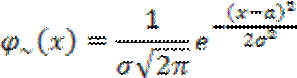
Кривую по нормальному закону распределения называют кривой Гаусса. Она имеет максимум в т.a с ординатой

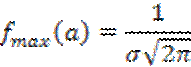
две точки перегиба:

 с ординатами

Кривая симметрична относительно прямой x=a, где a=M(x) и

Функция распределения выражается в виде:

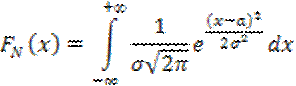
4.  Основной закон распределения – логарифмический нормальный закон распределения (логонормальный)

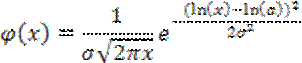
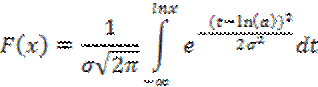
Данные сигналы отличаются уровнем вокруг которых происходят колебания. Этот уровень характеризует наиболее вероятное значение случайной величины.

Математическое ожидание – это наиболее вероятное значение случайной величины.

Для непрерывной случайной величины математическое ожидание определяется:

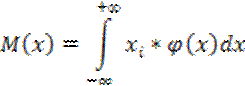
Основной характеристикой случайной величины является математическое ожидание:

                                   

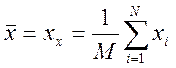
Случайные величины x₁(t) и x₂(t) колеблются на одном уровне, но имеют разные диапазоны колебаний (коридоры). Случайная величина x₂(t) имеет большую амплитуду колебаний, а значит большее отклонение от средней величины.

Дисперсия – «рассеяние» случайной величины.

Дисперсией D(x) случайной величины называется математическое ожидание квадрата ее отклонений от математического ожидания случайной величины.

Для нормального закона распределения дисперсия рассчитывается по формуле: