Сущность измерения. Идеализированная блок-схема. Метрологическое обеспечение производства. Основные преимущества использования адаптивных систем. Универсальные средства измерений, страница 10

S=R/d_n

где d_n - зависит от объема выборки.

Оценки параметров распределения не является точностными, так как зависят от объема выборки, определяют с той или иной вероятностью Р. Таким образом, доверительные пределы для ₀ по значениям опытного

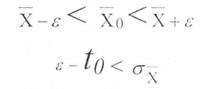
где to выбирается из таблиц.

Пример 1. Имеем 5 результатов измерений: 49,94; 49,90; 49,98; 49,95; 49,93. Вычислить доверительные пределы для оценки ₀. Подсчитаем = 49,94.

 

to - из таблицы, в зависимости от числа степеней свободы   K=n-1; K=5-1=4 и доверительной вероятности Р(to)=0,95, тогда to=2,776:   ε=2, 776-0,0156=0,04202,

где  - среднеквадратичное отклонение выборки.

 

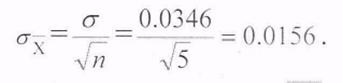           Определим пределы возможных отклонений :

 

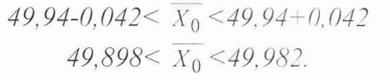Л-9

Анализ точности технологического процесса,

технологического оборудования.

С целью внедрения статистической управляемости технологического процесса необходимо знание закона распределения размерного параметра, что выполнимо на основе выборочной оценки. Наилучший отбор действий получается путем случайного отбора (таблицы случайных чисел). Объем выпуска 25-200 экземпляров.

Оценку соответствия опытного распределения предполагаемому производят по критериям согласия. Наиболее часто критерий Пирсона.

Поскольку теоретически доказано, что при обработке на станках размерные параметры в пределах 5÷6 квалитетов и нормально отклоняемой ТС, подчиненные нормальному распределению, в случае получения отрицательных результатов относительно закона распределения, необходимо технологический процесс отмерить до уровня статической управляемости.

С этой целью анализируется точность и закон распределения по каждой единицы технологического оборудования. Методика аналогична: берется выборка, считаются числовые характеристики, проверяемые закон распределения, при этом точность технологической системы по каждой единицы технологического оборудования должно быть δ≥ω, где δ - технологический допуск, ω = 65 - поле рассеяния исследуемого размерного параметра (для нормального закона). Для других равновероятен закон Максвелла, в соответствии с предполагаемым законом.

Подробная методика статистического анализа точности излагается в ГОСТах.

Статистическое регулирование точности процессов

механической обработки.

Регулирование точности процессов механической обработки ведется с использованием мгновенных выборок.

Мгновенной называется выборки из потока продукции, которая составляется в течение наименьшего интервала времени. Объем таких выборок не более 10 штук и, следовательно, этот метод называется метод малых выборок.

Статистическими характеристиками малых выборок являются выборочные средние , выборочные среднеквадратические отклонения S, выборочный размах R.

          Регулирование точности (управление точности) производится путем изучения систематической δ_сист и случайных погрешностей в  i - момент обработки. При этом

т.е. определима по значениям центров погрешностей управляемых параметров.

            ГОСТ 16.305-81 рекомендует подобным образом контролировать точность в условиях серийного и массового производств.

При нормальном законе распределения за величину мгновенного поля рассеяния примем ωi=6S_mimгде S-среднеквадратичное отклонение, определенное по мгновенной выборке.

Процесс считается точным, если перед очередной подналадкой

            Статистическое управление уровнем наладки осуществляется при условии на основе предварительного анализа, получены следующие данные:

 S - полученное из ряда выборок

- среднее значение

   -предельно допустимое выборочное среднее, соответствующее максимально допустимой доле брака, при появлении такого  - процесс следует корректировать.

            δ_см  - нормированное смещение наладки технологического процесса

Процесс      считается      налаженным,      если      =      и      разлаженным, если ==+δ_см или ==- δ_см

Составляется план статического регулирования: