2. Производим пересчет плотности газов при температуре отходящих газов Т К по формуле:
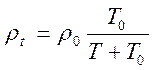 , (2.4.)
, (2.4.)
где ![]() t – плотность газа, кг/м3
(при данной температуре T К);
t – плотность газа, кг/м3
(при данной температуре T К);
Т-температура отходящих газов, К;
Т0- температура при нормальных условиях, Т0=273 К;
![]() 0-плотность газа при нормальных условиях, кг/м3
(t0 = 00C, p0
=101325 Па).
0-плотность газа при нормальных условиях, кг/м3
(t0 = 00C, p0
=101325 Па).
Плотность SО2 при Т = 623 К равна:
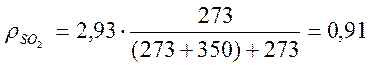 кг/м3;
кг/м3;
Плотность О2 при Т = 623 К равна:
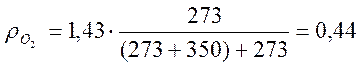 кг/м3;
кг/м3;
Плотность N2 при Т = 623 К равна:
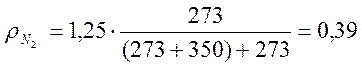 кг/м3.
кг/м3.
Плотность H2O при Т = 623 К равна:
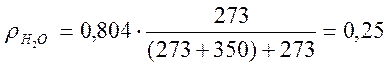 кг/м3.
кг/м3.
3. Рассчитаем плотность смеси газов γсм, используя следующую формулу:
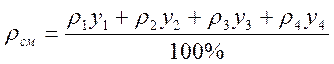 , (2.5.)
, (2.5.)
где ![]() i - плотность каждого компонента смеси
газов, кг/м3;
i - плотность каждого компонента смеси
газов, кг/м3;
![]() см - плотность смеси газов, кг/м3 (при
данной температуре T, К);
см - плотность смеси газов, кг/м3 (при
данной температуре T, К);
уi - объемное содержание каждого газа в смеси, %.
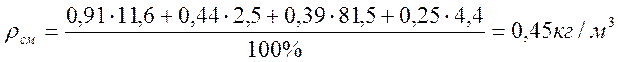
4. Для определения скорости седиментации используется формула, справедливая для ламинарного режима движения частиц сферической формы в однородной вязкой среде (по закону Стокса)[8]:
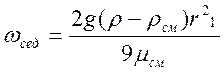 , (2.6.)
, (2.6.)
где ![]() - плотность пыли, кг/м3;
- плотность пыли, кг/м3;
![]() см - плотность смеси газов
при данной температуре отходящих газов, кг/м3;
см - плотность смеси газов
при данной температуре отходящих газов, кг/м3;
g - ускорение свободного падения, м/с2;
µсм - коэффициент динамической вязкости смеси при данной температуре T К;
r - радиус частиц пыли, м.
Скорость седиментации
частиц радиусом r1 = 7,6![]() -6м:
-6м:
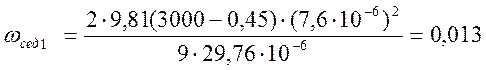 м/с
м/с
Скорость седиментации
частиц радиусом r2 = 42![]() -6м:
-6м:
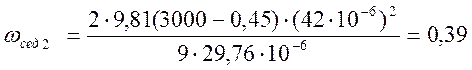 м/с
м/с
Скорость седиментации
частиц радиусом r3 = 102,2![]() -6м:
-6м:
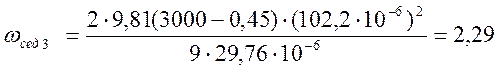 м/с
м/с
При пропускании запыленного газового потока через сильное электрическое поле частицы получают электрический заряд и ускорение, заставляющие их двигаться вдоль силовых линий поля с последующим осаждением на электродах. Вследствие того что силы, вызывающие осаждение частиц пыли, приложены только к этим частицам, а не ко всему потоку газа, расход энергии при электрической очистке значительно ниже, чем в большинстве других пылеулавливающих аппаратов.
Различают несколько способов зарядки:
Ø механическая, химическая или тепловая;
Ø индукционная (зарядка в близи поверхности электрода);
Ø ионная (зарядка в результате осаждения на частицах газовых ионов).
Ионная зарядка подразделяется на:
Ø ударную;
Ø диффузионная.
Ударная ионная зарядка – частицы заряжаются в результате удара об них движущихся ионов и их удержания на поверхности частиц «силами зеркального отображения». Этот режим зарядки характерен для частиц размером несколько мкм.
Диффузионная зарядка возникает вследствие разной концентрации ионов около частицы, что вызывает диффузию ионов к частице. В свою очередь, разность концентраций вызывается самой диффузией («поглощением» ионов частицей и кулоновскими силами отталкивания). Данный режим характерен для частиц размером менее 1мкм.
В данной работе проводятся расчеты для трех крупностей частиц, радиусы которых превышают 1 мкм, следовательно, для этих частиц превалирующим является механизм ударной ионной зарядки.
Рассчитаем скорость ударной зарядки для трех крупностей частиц.
Предельный заряд, который получает частица в результате ударной ионной зарядки, рассчитывается по формулам:
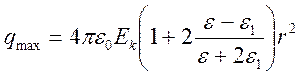 , (2.7.)
, (2.7.)
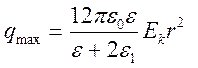 , (2.8.)
, (2.8.)
где ε - диэлектрическая проницаемость частиц;
ε0 - диэлектрическая постоянная, Ф/м; ε0 =
8,85![]() -12 Ф/м.
-12 Ф/м.
ε1 - диэлектрическая проницаемость газа;
Ек - электрическая напряженность внешнего электрического поля, В/м.
Скорость зарядки определяется по формуле Потенье:
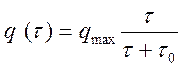 , (2.9.)
, (2.9.)
где τ0 - постоянная зарядки, с.
Постоянная зарядки определяется по формуле:
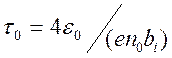 , (2.10.)
, (2.10.)
где е - электрический заряд, е = 1,6![]() -19
Кл;
-19
Кл;
n0 - концентрация ионов, ионов/м3.
bi - подвижность ионов, м2/В![]() .
.
Подвижность ионов bi определяется зависимостью Нернста-Таундсенда:
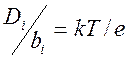 , (2.11.)
, (2.11.)
где Di - коэффициент диффузии, м2/с;
k - константа Больцмана, k=1,38![]() -23 Дж/К.
-23 Дж/К.
Формула Эйнштейна
![]() , (2.12.)
, (2.12.)
Закон Эйнштейна-Смолуховского:
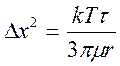 , (2.13.)
, (2.13.)
Из этих формул выразим коэффициент диффузии:
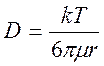 , (2.14.)
, (2.14.)
где µ- коэффициент динамической вязкости, Па![]() [8].
[8].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.