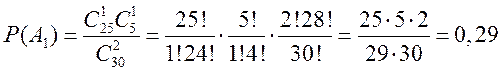
Вероятность того, что среди двух взятых лампочек обе бракованные
(![]() ), равна
), равна
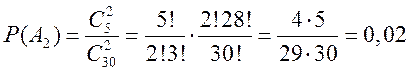 .
.
Составим ряд распределения:
|
|
0 |
1 |
2 |
|
|
0,69 |
0,29 |
0,02 |
Если возможных значений дискретной случайной величины достаточно много, то используют другой способ ее задания: с помощью функции распределения. Этот способ применяется и для задания непрерывной случайной величины.
Функцией распределения
называется функция ![]() равная вероятности того, что
случайная величина
равная вероятности того, что
случайная величина ![]() примет значение меньше данного
примет значение меньше данного ![]() :
: ![]() .
.
Пример: составить функцию распределения по условиям предыдущей задачи .
Решение.
Так как по условию ![]() не принимает значений меньших
нуля, то вероятность события
не принимает значений меньших
нуля, то вероятность события ![]() при
при ![]() равно нулю (невозможное событие).
равно нулю (невозможное событие).
При ![]() вероятность
события
вероятность
события ![]() равна 0,69 так как в этом случае случайная
величина
равна 0,69 так как в этом случае случайная
величина ![]() может иметь только значение 0 с вероятностью
0,69.
может иметь только значение 0 с вероятностью
0,69.
В промежутке ![]() вероятность события
вероятность события ![]() будет равна сумме вероятностей
0,69+0,29=0,98, так как в этом случае случайная величина может принимать два
значения 0 и 1.
будет равна сумме вероятностей
0,69+0,29=0,98, так как в этом случае случайная величина может принимать два
значения 0 и 1.
Рассуждая аналогично, получим,
что вероятность события ![]() при
при ![]() равна сумме 0,69+0,29+0,02=1.
равна сумме 0,69+0,29+0,02=1.
Запишем функцию распределения в виде
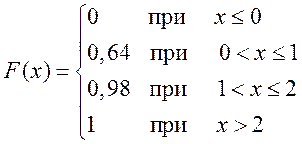
3.4 Основные понятия математической статистики
В любой сфере человеческой деятельности приходится иметь дело со случайными величинами.
В математической статистике всю совокупность элементов, подлежащих обследованию, называют генеральной совокупностью. Часть генеральной совокупности называют выборкой.
Значения случайной величины называют вариантами. На первом этапе статистического исследования составляют вариационный ряд, то есть варианты упорядочивают в порядке возрастания (операция ранжирования).
Если числовых
значений случайной величины много, то для удобства производят группировку
вариант, то есть объединяют их в интервалы. Таким образом, получается аналог
непрерывной случайной величины. Каждому интервалу соответствует определенная
частота ![]() , которая показывает, сколько раз встречаются
варианты из данного интервала. Кроме того, используется понятие относительной
частоты, то есть отношение
, которая показывает, сколько раз встречаются
варианты из данного интервала. Кроме того, используется понятие относительной
частоты, то есть отношение 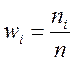 , где n
– объем выборки.
, где n
– объем выборки.
Пример. Дана статистическая совокупность, характеризующая время решения контрольной работы.
|
38 |
60 |
41 |
51 |
33 |
42 |
45 |
21 |
53 |
60 |
|
68 |
52 |
47 |
46 |
49 |
49 |
14 |
57 |
54 |
59 |
|
77 |
47 |
28 |
48 |
32 |
32 |
42 |
58 |
61 |
30 |
|
61 |
35 |
47 |
72 |
45 |
45 |
44 |
55 |
30 |
40 |
|
67 |
65 |
39 |
48 |
10 |
10 |
42 |
59 |
50 |
54 |
Требуется сгруппировать выборку в
виде интервального ряда с длиной интервала ![]() мин,
построить вариационный ряд.
мин,
построить вариационный ряд.
Решение. Упорядочив варианты в порядке возрастания от 10 до 80 и объединив их в интервалы длиной 10 мин, получим следующий вариационный ряд:
|
|
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
|
|
2 |
2 |
7 |
18 |
12 |
7 |
2 |
Способы обработки выборки
Для описания случайной
величины используют числовые характеристики. К ним относятся: выборочная
средняя ![]() , дисперсия
, дисперсия ![]() и
среднее квадратическое отклонение
и
среднее квадратическое отклонение ![]() .
.
Выборочная средняя служит оценкой (приближенным значением) генеральной средней и находится по формуле:
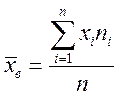 .
.
Дисперсия![]() и среднее квадратическое
и среднее квадратическое ![]() служат мерой оценки рассеяния всех
значений случайной величины вокруг ее среднего значения. Они находятся по формулам:
служат мерой оценки рассеяния всех
значений случайной величины вокруг ее среднего значения. Они находятся по формулам:
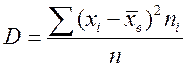 ;
; ![]() .
.
На практике для вычисления дисперсии проще использовать формулу:
![]() , где
, где 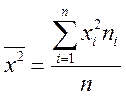 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.