Новая переменная выбирается таким образом, чтобы преобразованный интеграл оказался табличного вида.
Пример:

Метод интегрирования по частям основан на формуле
![]() .
.
При этом подынтегральное выражение делят на две части. Одну
обозначают ![]() , другую
, другую ![]() .
.
Затем находят ![]() и
и ![]() . Выделять части нужно так, чтобы новый
интеграл
. Выделять части нужно так, чтобы новый
интеграл ![]() оказался проще исходного.
оказался проще исходного.
Пример:
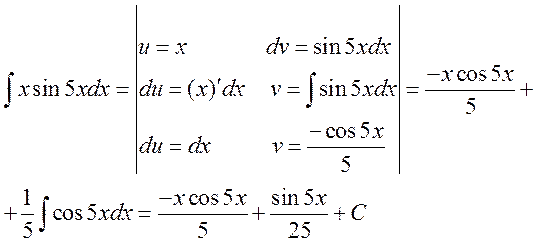
Определенный интеграл вычисляется с помощью тех же методов, что и неопределенный, но при этом используется формула Ньютона - Лейбница.
Пример:
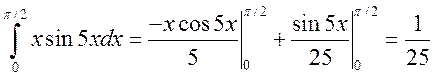 .
.
Геометрический смысл определенного интеграла ясен из рисунка 6 и формулы
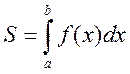 ,
,
где ![]() -
площадь криволинейной трапеции.
-
площадь криволинейной трапеции.
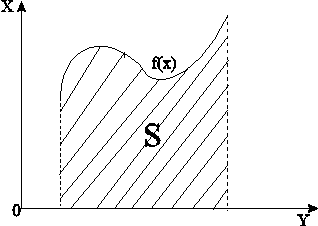
Рис.6
Пример:
Найти площадь фигуры (рис.7), ограниченной параболой ![]() и
осью
и
осью ![]() .
.
Решение: Найдем
пределы интегрирования как точки пересечения параболы ![]() с
осью
с
осью ![]() .
.
При ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теперь найдем площадь как
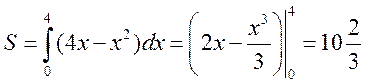 (кв.ед.)
(кв.ед.)
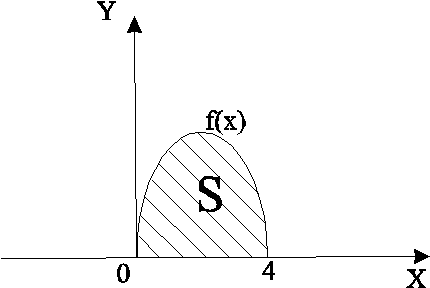
Рис.7
Площадь
фигуры, заключенной между двумя линиями ![]() и
и ![]() , вычисляется по формуле:
, вычисляется по формуле:
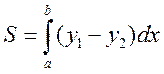 .
.
Упражнения
1. Вычислить интеграл:
1. ∫![]() 2.
∫
2.
∫ 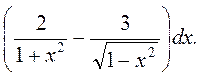
3. ∫ 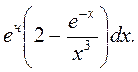 4.
∫
4.
∫ ![]()
5. ∫ ![]() 6.
∫
6.
∫ ![]()
7. ∫ ![]() 8.
∫
8.
∫ ![]()
9. ∫ ![]() 10.
10.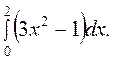
11. ![]() 12.
12.
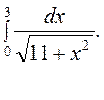
13. 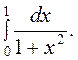 14.
14.
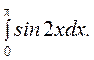
2. Вычислить площади фигур, ограниченных линиями:
1. ![]() 2.
2.![]()
3. ![]() 4.
4.
![]()
5. ![]() 6.
6. ![]()
7. 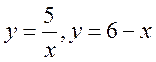 8.
8.![]()
3 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
3.1 Случайные события
Теория вероятностей - это раздел математики, в котором изучаются случайные события и выводятся закономерности, которым они подчиняются при массовом повторении.
Под событием
понимается любой результат опыта или наблюдения. События принято обозначать
первыми заглавными буквами латинского алфавита: ![]()
События делятся на три вида:
- достоверные, те, которые обязательно произойдут при определенных условиях;
- невозможные, те, которые заведомо не произойдут при определенных условиях;
- случайные, те, что могут произойти или не произойти при определенных условиях.
События можно складывать и умножать.
Суммой событий называется новое событие, состоящее в том, что происходит хотя бы одно из слагаемых событий.
Произведением событий называется новое событие, состоящее в том, что происходят все перемножаемые события.
Пример: из двух лотерейных
билетов выигрышным является первый- событие А, выигрышным является второй
билет - событие В. Тогда событие А + В состоит в том, что выиграет либо первый
билет, либо второй, либо оба билета. Событие ![]() состоит
в том, что выиграют оба билета.
состоит
в том, что выиграют оба билета.
Геометрически операции над событиями изображаются с помощью кругов Эйлера (рис 8)
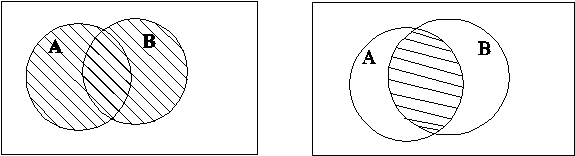
А +
В ![]()
Рис.8.
Классификация событий
События называются совместимыми, если в результате опыта возможно появление всех этих событий. События называются несовместимыми, если возможно появление только одного из них.
Два
несовместимых события называются противоположными, если в условиях опыта
одно из них обязательно произойдет. Противоположные события обозначаются как ![]() .
.
Понятие вероятности
Вероятность
служит количественной мерой объективной возможности появления события и
обозначается символом ![]() .
.
Вероятность события находится по формуле
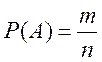 ,
(1)
,
(1)
где ![]() - число
исходов опыта, благоприятствующих наступлению данного события,
- число
исходов опыта, благоприятствующих наступлению данного события,
![]() - общее число исходов опыта.
- общее число исходов опыта.
Заметим, что вероятность достоверного события равна 1, вероятность невозможного события равна 0. Вероятность противоположного события находится по формуле:
![]() .
.
Пример. В лотерее играет 1000 билетов. Из них 20 билетов выигрышных. Какова вероятность приобрести выигрышный билет - событие А?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.