Информатика и математика (Математика): Учебно-методический комплекс, страница 3

3.                                                         4.

5.                                                 6.

7.                                            8.

9.                                                       10.

3. Представить сложную функцию в виде цепочки элементарных функций.

1.                                                 2.

3.                                                    4.

5.                                               6.

7.                                                  8.

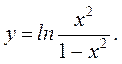 9.                                               10.

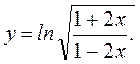
2.2 Дифференциальное исчисление

Во многих практических задачах требуется определить скорость изменения функции при изменении аргумента. В этом случае используется понятие производной функции. Это понятие в свою очередь вводится с помощью понятия предела функции. Поясним смысл понятия предела на примере.

Функция 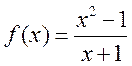    не определена при , при котором знаменатель обращается в нуль. Таким образом, при  функция имеет разрыв  (рис.4).

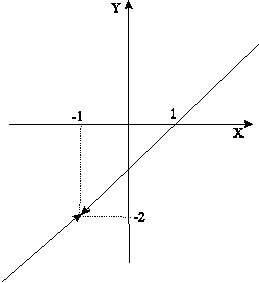
Рис.4

Однако если положить значение функции в точке   равным  -2, то получим функцию непрерывную на всей числовой оси. Математически это записывается как

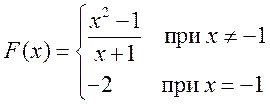
В общем случае, если - точка разрыва функции , но возможно найти для нее в точке  такое значение  А, при котором измененная функция станет непрерывной, то это число  А называется пределом функции   в точке , а  точка -точкой устранимого разрыва.

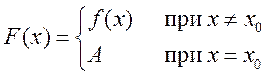
Математически это записывается формулой:

Существование предела функции  в точке  означает,  что функция   приближенно равна   для всех  значений , близких к . Заметим, что если функция непрерывна в точке , то предел функции равен значению функции в этой точке:

Перейдем теперь к понятию производной.

      Производной функции в точке  называется предел отношения  приращения функции  к приращению аргумента  при условии, что последнее стремится к нулю:

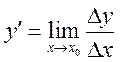
Разберем смысл этого понятия. Учитывая смысл понятия предела, можно записать

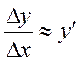 или .

Отсюда следует, что  является коэффициентом пропорциональности между приращением функции  и приращением аргумента , который показывает, как изменяется функция при изменении аргумента на единицу.

Механический смысл производной - это мгновенная скорость точки.   Геометрический смысл производной - это угловой коэффициент  касательной к графику функции в точке с абсциссой .

В общем случае, производная - это скорость изменения функции.

Нахождение производной называется дифференцированием функции. Производная функции находится с помощью таблицы  и основных правил дифференцирования.

Таблица производных

Функция	Производная
	0

Правила дифференцирования

Пусть функции   и  имеют производные, тогда справедливы следующие правила.

 Производная алгебраической суммы функций равна алгебраической сумме производных этих функций:              

.

Производная произведения двух функций находится по формуле:

.

Производная частного вычисляется по формуле:

.

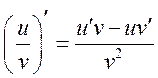Производная сложной функции , где  находится по  формуле

Пример.  Найти производные функций: ; .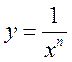

Решение. Используя данные таблицы производных, получим:

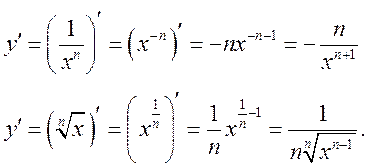
Пример.  Найти производные функций:

                  .

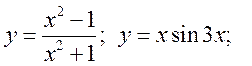Решение. Используя данные таблицы производных и правила дифференцирования, получим:

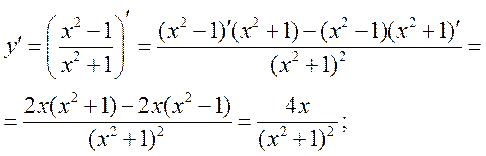
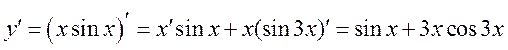
2.3 Использование производных для исследования

функций

Достаточное условие возрастания и убывания функции.

Если в некотором промежутке производная данной функции больше нуля , то  функция возрастает в этом промежутке; если производная меньше нуля  ,  то функция убывает.