Информатика и математика (Математика): Учебно-методический комплекс, страница 7

      а) тома стоят по порядку (в любом направлении);

      б) пятый и третий том стоят рядом.

2. На стеллаже 20 учебников, 7 из них в переплете. Наугад выбирают 4 учебника. Какова вероятность того, что все они будут в переплете?
3. Собрание, состоящее из 30 человек, среди которых 8 женщин, выбирает делегацию из 3 человек. Найти вероятность того, что в делегацию войдут двое мужчин и одна женщина.
4. Набирая номер телефона, вы забыли одну цифру и набрали ее наудачу. Найти вероятность того, что будет набрана нужная цифра?
5. На карточке спортлото написаны числа от 1 до 49. Какова вероятность того, что наугад зачеркнутое число на этой карточке кратно 6?
6. В роте 90 курсантов, из них 30 учатся на 4 и 5. Какова вероятность того, что выбранный наудачу курсант учится на 4 и 5?
7. В наборе конфет 10 содержат начинку, а 6 не содержат. Из набора выбирают 8 конфет. Какова вероятность того, что из них ровно половина конфет с начинкой?
8. В партии из 40 деталей 4 оказались с дефектами. Какова вероятность того, что из 3 взятых наудачу деталей одна деталь с дефектом?
9. Найти вероятность того, что участник лотереи «Спортлото – 6 из 49», купивший один билет, угадает правильно 6 номеров.
10. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что:

а) все они одного цвета;

б) все они разных цветов;

в) среди них 2 синих и 1 зеленый карандаш.

3.2 Теоремы сложения и умножения вероятностей

Кроме формул комбинаторики для нахождения вероятности применяются теоремы.

Теорема сложения.  Вероятность суммы несовместных событий равна сумме вероятностей этих событий:

.

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения:

.

Отметим, что последняя формула применяется для нахождения вероятности появления хотя бы одного из слагаемых событий.

Если требуется найти вероятность совместного появления событий, то используется теорема умножения. При этом вводятся понятия условной вероятности и независимых событий.

Вероятность события В, найденная при условии, что событие А произошло называется условной вероятностью и обозначается как .

Событие. В называется независимым от события  А, если его вероятность не меняется от того, произошло событие  А  или нет.

Теорема умножения. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

.

Для независимых событий теорема упрощается и записывается в виде:

.

При решении задач часто используются обе теоремы совместно.

Примеры решения задач

Задача 1. Первый стрелок поражает мишень с вероятностью 0,9, второй – 0,8. Найти вероятность того, что в мишень попадет хотя бы один стрелок.

Решение. Обозначим события  -  в мишень попал первый стрелок,  - в мишень попал второй стрелок,  – в мишень попал хотя бы один стрелок. Так как события совместны, то можно использовать теорему сложения для совместных событий.

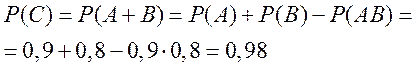
Можно использовать и другой способ: сначала найти вероятность того, что оба стрелка промахнулись

.

А затем найти искомую вероятность, как вероятность противоположного события

.

Задача 2. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Решение. Обозначим событие, состоящее в появлении двух белых шаров подряд, буквой . Событие  представляет собой произведение двух событий: , где  - появление белого шара при первом вынимании;  - появление белого шара при втором вынимании. События  и зависимы. Применяя теорему о произведении зависимых событий, получаем:

.

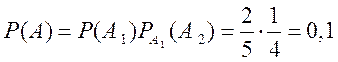Задача 3. Фирма приобрела две партии товара. В первой партии 20 цветных и 5 белых изделий; во второй партии 12 цветных и 3 белых изделия. Наугад выбирают по одному изделию из каждой партии. Какова вероятность того, что только одно из взятых изделий цветное.