Определение экстремума функции.
Точками экстремума функции называются точки максимума и минимума. На конечном промежутке у функции может быть несколько максимумов и минимумов, то есть экстремум имеет локальный характер.
Необходимое условие экстремума
Если ![]() является точкой экстремума функции
является точкой экстремума функции ![]() , то ее первая производная
, то ее первая производная ![]() в этой точке равна нулю или не существует.
Точки экстремума называются критическими точками.
в этой точке равна нулю или не существует.
Точки экстремума называются критическими точками.
Достаточное условие экстремума
Если производная
функции при переходе через критическую точку ![]() меняет
знак с плюса на минус, то есть
меняет
знак с плюса на минус, то есть
![]() при
при ![]() и
и ![]() при
при ![]() ,
,
то функция в этой точке имеет максимум.
Если производная функции при переходе через критическую точку меняет знак с минуса на плюс, то есть
![]() при
при ![]() и
и ![]() при
при ![]() ,
,
то в этой точке функция имеет минимум.
Пример. Найти интервалы
возрастания и убывания и экстремум функции ![]() .
.
Решение. Находим производную функции:
![]() .
.
Решая уравнение ![]() , получаем две точки возможного экстремума
, получаем две точки возможного экстремума ![]() и
и ![]() .
.
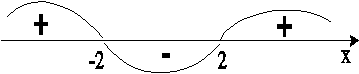
Рис.5
Исследовав
знак ![]() (рис.5), получаем, что на интервалах
(рис.5), получаем, что на интервалах ![]() и
и ![]() функция
функция
![]() возрастает, а на интервале
возрастает, а на интервале ![]() - убывает.
- убывает.
Точка ![]() - точка максимума,
- точка максимума, ![]() -
максимальное значение функции, а точка
-
максимальное значение функции, а точка ![]() - точка
минимума,
- точка
минимума, ![]() - минимальное значение функции.
- минимальное значение функции.
Упражнения
1. Найти производные функций:
1. ![]() 2.
2.
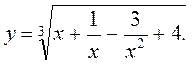
3. ![]() 4.
4.
![]()
5. ![]() 6.
6.
![]()
7. ![]() 8.
8.
![]()
9. 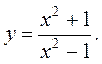 10.
10.
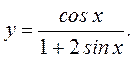
2. Найти промежутки монотонности и экстремумы следующих функций:
1. ![]() 2.
2.
![]()
3. 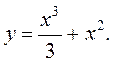 4.
4.
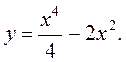
5. 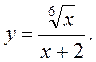 6.
6. 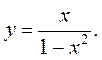
7. 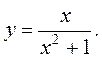 8.
8.
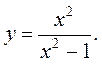
9. ![]() 10.
10. ![]()
2.4 Интегральное исчисление
В тех задачах, где требуется найти суммарное значение некоторой непрерывной функции на данном промежутке, используется операция интегрирования. Операция интегрирования является обратной для операции дифференцирования.
Постановка задачи.
Найти такую функцию ![]() , производная которой равна
данной функции
, производная которой равна
данной функции ![]() , то есть
, то есть
![]()
Функция ![]() называется
первообразной для функции
называется
первообразной для функции ![]() .
.
Совокупность всех первообразных называют неопределенным интегралом функции, и обозначают как
![]() ,
,
где С - произвольная
постоянная, ![]() - дифференциал независимой переменной.
- дифференциал независимой переменной.
Заметим, что
дифференциалом функции ![]() называют произведение
производной этой функции на дифференциал независимой переменной, то
есть
называют произведение
производной этой функции на дифференциал независимой переменной, то
есть
![]() .
.
Если требуется
найти приращение первообразной на некотором отрезке ![]() ,
то используется определенный интеграл:
,
то используется определенный интеграл:
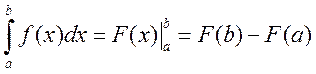 .
.
Эта формула называется формулой Ньютона- Лейбница.
Заметим, что неопределенный интеграл - это функция, а определенный интеграл - это число.
Для вычисления интегралов используются таблица основных интегралов и свойства интегралов.
Таблица интегралов
|
1. |
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
|
9. |
10. |
|
11. |
12. |
Свойства интегралов
1. Интеграл от дифференциала функции равен самой функции
![]()
В частности,
![]() +C
+C
2. Постоянную можно выносить за знак интеграла:
![]() .
.
3 . Интеграл суммы функций равен сумме интегралов этих функций:
![]()
Метод вычисления интегралов, основанный на свойствах интеграла, называется методом непосредственного интегрирования. При этом часто нужно сначала сделать элементарные преобразования подынтегральной функции.
Пример:
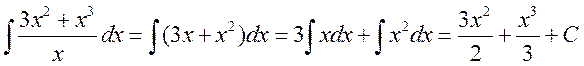 .
.
Если не удается путем преобразования функции привести интеграл к табличному виду, то для его вычисления используются другие методы интегрирования.
Метод
замены переменной основан на введении новой переменной ![]() .
.
Это можно сделать одним из двух способов:
или ![]() , а
, а 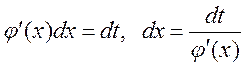 ,
,
или ![]() , а
, а ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.