Информатика и математика (Математика): Учебно-методический комплекс, страница 10

Второй способ описания случайной величины - графический с помощью полигона и гистограммы.

     Полигон частот строят следующим образом: на оси абсцисс откладывают варианты , а на оси ординат  соответствующие им частоты . Полученные точки соединяют ломаной линией. Аналогично строят полигон относительных частот.

 Гистограмма частот представляет собой ступенчатую фигуру из прямоугольников, основаниями которых служат частичные интервалы длиной   , а высоты равны отношению частоты интервала к его длине . Аналогично строят гистограмму относительных частот.

      Заметим,  что обычно для изображения дискретного  распределения используют полигон, а для изображения непрерывного - гистограмму.

Пример. Вычислить среднюю, дисперсию, среднее квадратическое отклонение, построить полигон частот для следующей выборки:

	38	39	40	41	41	43
	3	9	26	31	37	11	Итого: 117

Решение. Найдем выборочную среднюю:

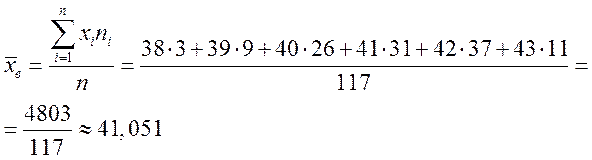
Дисперсию найдем по формуле , где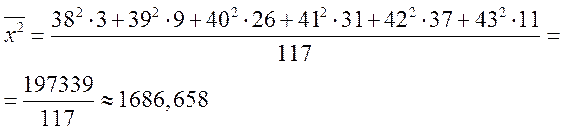

Итак, .

Найдем среднее квадратическое отклонение:

.

Построим полигон частот (рис.9):

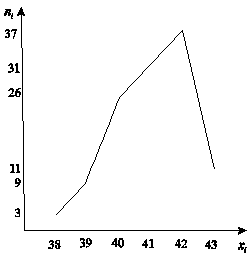
Рис.9.

Пример. Дано непрерывное распределение некоторой величины:

Вычислить среднюю, дисперсию, среднее квадратическое отклонение, построить гистограмму частот.

Решение. Приведем непрерывное распределение к дискретному путем замены интервала значений его серединой. Получим следующее распределение:

Найдем объем выборки по формуле : .

Найдем выборочную среднюю:

.

Найдем дисперсию: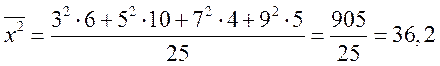

Итак, .

Найдем среднее квадратическое отклонение:

.

Построим гистограмму частот. Для этого построим на оси  заданные интервалы длиной . Проведем над этими интервалами отрезки, параллельные оси  и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты .

Искомая гистограмма изображена на рис. 10.

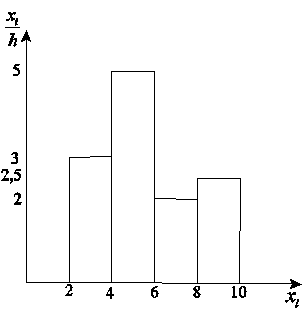
Рис. 10

Упражнения

1.Вычислить среднюю, дисперсию, среднее квадратическое отклонение, построить гистограмму частот или полигон частот следующих случайных величин.

1.

	1	4	6	8
	10	15	25	5

 2.

	15	20	25	30	35
	10	15	30	20	25

3.

	2	4	5	7	10
	15	2	1	1	45

4.

	20	60	75	100	150	250
	9	34	26	71	32	2

5.

	2	4	6	8	10	12
	2	64	154	128	78	20

6.

	10-15	15-20	20-25	25-30	30-35
	2	4	6	4	2

7.

	44-46	46-48	48-50	50-52	52-54
	17	20	11	7	4

8.

	40-50	50-60	60-70	70-80	80-90
	33	63	28	11	6

9.

	11-13	13-15	15-17	17-19	19-21
	8	41	52	37	12

10.