В данном случае
, а 
. Тогда
по формуле имеем
.
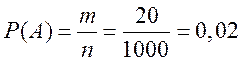Вероятность противоположного события, то есть вероятность
приобрести невыигрышный билет равна: 
.
Формулы комбинаторики.
Часто для
нахождения 
и 
в
формуле (1) применяется одна из формул комбинаторики: перестановки,
размещения или сочетания.
Комбинации из
элементов, которые отличаются только
порядком расположения этих элементов, называются перестановками из элементов. Число перестановок находится по
формуле:
(2).
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Поскольку каждый вариант жеребьевки отличается только порядком участников конкурса , то их число находится как перестановки из 7 элементов:
= 5040.
Комбинации из элементов по ,
которые отличаются только составом элементов называются сочетаниями.
Число сочетаний из элементов по находится по формуле:
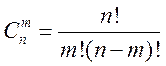(3).
Пример. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна только одна партия?
Поскольку каждая партия играется двумя участниками из 16 и отличается от других только составом участников, то число партий находится как сочетания из 16 элементов по 2.
.
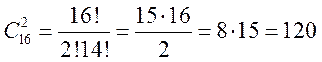Комбинации из элементов по ,
которые отличаются либо составом, либо порядком расположения элементов, называются
размещениями из элементов по . Число размещений находится по формуле:
или 
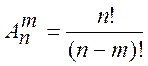(4).
Пример. Расписание одного учебного дня состоит из 5 дисциплин. Определить сколько вариантов расписания можно составить из 11 дисциплин.
Поскольку каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом, так и порядком следования дисциплин, то число вариантов находится как размещение из 11 элементов по 5:
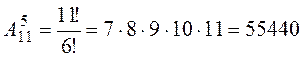
Упражнения
1. Задачи на использовании формул комбинаторики.
1. Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4,5 при условии, что ни одна цифра не повторяется более одного раза?
2. Автомобильные номера составляются из трех букв и трех цифр. Найти число таких номеров.
3. Набирая номер телефона, вы забыли последние две цифры, но помните, что они различны. Сколько вариантов из 10 цифр по 2 вам придется перебрать, если будете набирать наугад?
4. В розыгрыше первенства страны по футболу принимает участие 16 команд. Сколькими способами медали могут быть распределены между командами?
5. В математическом кружке 25 человек. Необходимо выбрать председателя кружка, его заместителя, редактора стенгазеты и секретаря. Сколькими способами можно избрать эту руководящую четверку, если одно лицо может занимать только один пост?
6. На конференции должны выступать 5 докладчиков, причем докладчик A должен выступить раньше докладчика B. Сколькими способами можно установить очередность выступления?
7. Сколькими способами можно выбрать 2 розовые и 3 красные гвоздики из букета, содержащего 10 красных и 5 розовых гвоздик?
8. Некоторый комитет состоит из 14 человек. Минимальный кворум для принятия решения должен насчитывать 11 человек. Сколькими способами может быть достигнут какой-либо кворум?
9. Четыре автора должны написать книгу из 17 глав, причем первый и третий должны написать по 5 глав, второй – 4, а четвертый – 3 главы книги. Сколькими способами можно распределить главы между авторами?
10. Сколько трехзначных чисел, кратных двум можно составить из цифр 1,4,3,5,7,9 при условии, что цифры в числе не повторяются?
2. Задачи на непосредственный подсчет вероятности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.