Решение. Обозначим события:
![]() - взятое изделие из первой партии цветное.
- взятое изделие из первой партии цветное.
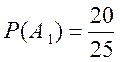 ;
; 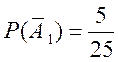 .
.
![]() - взятое изделие из второй партии
цветное.
- взятое изделие из второй партии
цветное.
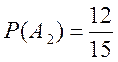 ;
; 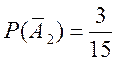 .
.
Тогда
вероятность события ![]() , состоящего в том, что только
одно из взятых изделий цветное, запишется формулой:
, состоящего в том, что только
одно из взятых изделий цветное, запишется формулой:
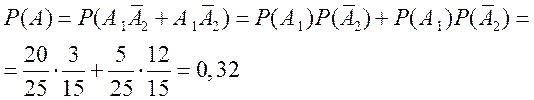 .
.
Упражнения
1.Решить следующие задачи, используя теоремы вероятностей.
а) только один баскетболист попадет в корзину;
б) хотя бы один баскетболист попадет в корзину;
в) все три баскетболиста попадут в корзину.
а) два вопроса; б) более двух вопросов.
3.3 Случайные величины
Случайная величина - второе основное понятие теории вероятностей. В отличие от случайного события случайная величина - это переменная, которая может принимать различные значения в зависимости от обстоятельств. Случайные величины делятся на два вида: дискретные и непрерывные.
Дискретными называются случайные величины, которые принимают отдельные значения.
Например, число, присутствующих на семинаре студентов из группы 25 человек может иметь значения 0, 1, 2,…..,25.
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого промежутка. Например, рост студентов в группе.
Способы задания случайных величин.
Дискретную случайную величину обычно задают с помощью закона (ряда) распределения, представленного в форме таблицы:
|
|
|
|
… |
|
|
|
|
|
… |
|
здесь ![]() - все
возможные значения случайной величины Х,
- все
возможные значения случайной величины Х, ![]() -
вероятности, с которыми эти значения принимаются.
-
вероятности, с которыми эти значения принимаются.
Пример. В упаковке из 30 лампочек имеется 5 бракованных. Наугад вынули 2 лампочки. Составить ряд распределения числа вынутых бракованных лампочек - Х.
Решение: ![]() - число бракованных лампочек может быть равно
0,1,2.
- число бракованных лампочек может быть равно
0,1,2.
Вероятность того, что среди двух взятых лампочек нет ни одной
бракованной (![]() ), равна
), равна
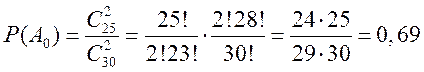
Вероятность того, что среди двух взятых лампочек только
одна бракованная (![]() ), равна
), равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.