Статистические оценки параметров распределения. Доверительный интервал, доверительная вероятность.
2 ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
2.1 Понятие функции
Математика - это наука о пространственных формах и количественных отношениях действительного мира. К основным понятиям математики относится понятие - величина. Под величиной понимается все, что может быть измерено в окружающем нас мире. В математике безразлична физическая сущность величины. Поэтому выводы математики применимы ко всем величинам вообще. Величины бывают постоянные и переменные. Между переменными величинами может существовать функциональная зависимость.
Переменная величина y называется функцией от переменной величины x, если каждому значению величины x по некоторому правилу ставится в соответствие определенное значение величины y.
Это
обозначается, как ![]() , при этом величина x называется независимой переменной (аргументом), а y - зависимой переменной, или функцией от переменной
, при этом величина x называется независимой переменной (аргументом), а y - зависимой переменной, или функцией от переменной ![]() .
.
Каждая функция имеет свою область определения, под которой понимается множество всех возможных значений аргумента.
Пример. Найти область определения функции
![]() .
.
Решение.
Так как функция представляет собой сумму функций, то область определения
функции будет состоять из всех тех значений ![]() ,
которые принадлежат одновременно области определения функций
,
которые принадлежат одновременно области определения функций ![]() и
и ![]() .
Поэтому область определения данной функции определяется как совокупность
значений
.
Поэтому область определения данной функции определяется как совокупность
значений ![]() , при которых одновременно выполняются
неравенства
, при которых одновременно выполняются
неравенства ![]() и
и ![]() . Это
будет значение
. Это
будет значение ![]() .
.
Для задания функции существует три способа.
1. Аналитический способ задания функции состоит в том, что соответствие между переменными задается с помощью формулы, например,
![]() ,
, ![]() и т.д.
и т.д.
В общем виде это записывается как
![]() или
или ![]() . Во
втором случае говорят, что функция задана неявно.
. Во
втором случае говорят, что функция задана неявно.
Функция
называется сложной, если ее аргумент сам является функцией: ![]() . В этом случае
. В этом случае ![]() называется
промежуточным аргументом.
называется
промежуточным аргументом.
Пример:
Представить сложную функцию ![]() в виде цепочки
элементарных функций.
в виде цепочки
элементарных функций.
Решение.
В функции ![]() возьмем
возьмем ![]() , тогда
получим элементарную функцию
, тогда
получим элементарную функцию ![]() .
.
2. Табличный способ задания функции состоит в том, что соответствие между переменными задается в виде таблицы.
Пример:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Y |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
3. Графический способ задания функции состоит в том, что соответствие между переменными задается в виде графика.
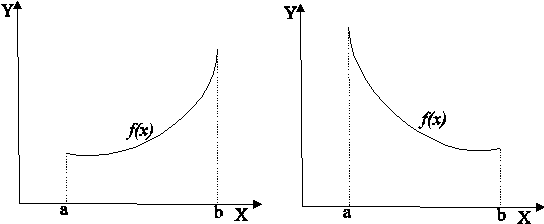
Рис.1 Рис. 2
На рис. 1 изображена возрастающая функция. На рис.2 изображена убывающая функция.
Важным свойством функции является непрерывность.
Функция
считается непрерывной, если малое изменение значения аргумента влечет
за собой малое изменение значения функции. Математически это записывается так:
при ![]()
Под ![]() и
и ![]() понимается приращение переменных, то есть
разность между последующим и предыдущим значениями:
понимается приращение переменных, то есть
разность между последующим и предыдущим значениями: ![]() ,
, ![]()
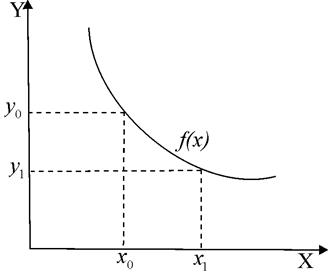
Рис.3
Упражнения
1. Найти область определения функций, заданных формулами:
1. у = 3х + 2. Ответ: (- ∞, + ∞).
2. у = х³ + 5х + 6. Ответ: (- ∞, + ∞).
3. у = 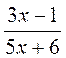 . Ответ:
(- ∞, 6/5), (6/5, + ∞).
. Ответ:
(- ∞, 6/5), (6/5, + ∞).
4. ![]() . Ответ:
х = 2.
. Ответ:
х = 2.
5. 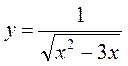 . Ответ:
(- ∞, 0), (3, + ∞).
. Ответ:
(- ∞, 0), (3, + ∞).
6. ![]() . Ответ:
[-2, 2].
. Ответ:
[-2, 2].
7. ![]() . Ответ:
(
. Ответ:
(![]() , + ∞﴿.
, + ∞﴿.
8. 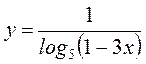 . Ответ:
(- ∞, 0), (0,
. Ответ:
(- ∞, 0), (0, ![]() ).
).
9. ![]() . Ответ:
(- ∞, 0), (0, + ∞).
. Ответ:
(- ∞, 0), (0, + ∞).
10. 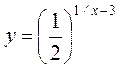 . Ответ:
(- ∞, 3), (3, + ∞).
. Ответ:
(- ∞, 3), (3, + ∞).
2. Построить графическое изображение функций.
1. ![]() 2.
2.
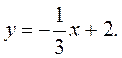
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.