Теория электрической связи: Конспект лекций. Часть 1, страница 8

  Спектр АИМ сигнала в соответствии с  формулой (3.5)  принимает вид, показанный на рис.3.11.                                           

                                                              

                                                                     _·

                                            S_д(w)

                                                                                                

 

 

                                                                                                                

              -2w_д         - w _д      - w_в           0              w_вw_д           2w_д     w

                                                                                    Рис.3.11

3.4. Восстановление непрерывного сигнала из отсчётов.

В линию связи передаются импульсы-отсчёты, которые поступают на вход приёмника.

Для восстановления исходного непрерывного сигнала из импульсов-отсчётов надо эти импульсы подать на вход идеального фильтра низких частот (ИФНЧ), который имеет следующие характеристики.

  Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:                                        

                                                 K(w)

                                           K

 

- w_д               0                     w_дw

                                                                                   Рис.3.12

Импульсная реакция ИФНЧ, т.е. реакция на дельта-импульс имеет вид:

                                                    g_ифнч (t)

 

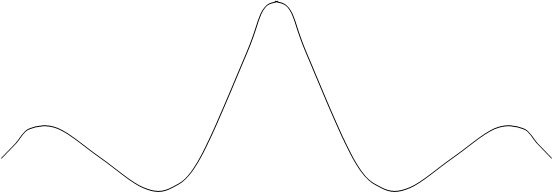                            Рис. 3.13   

                                                                    t

         -3 Dt     - 2Dt        -Dt       0        Dt           2Dt        3Dt  

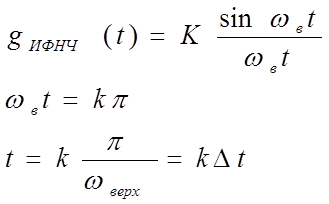                                 (3.6)

 Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых

g _ИФНЧ(t) обращается в ноль.

Cо спектральной точки зрения мы пропускаем дискретизированный сигнал, имеющий спектр в соответствии с рис.3.9 или 3.11, через ИФНЧ с АЧХ  рис.3.12. Очевидно, что на выходе ИФНЧ получим спектр:

         S(w)= K S_д(w) = K S_x(w) /Dt;

или для АИМ сигнала получим:  S(w)= KS_д(w) = K a₀S_x(w) /2.

Таким образом, с точностью до постоянного множителя мы получили на выходе ИФНЧ спектр исходного сигнала x(t). С временной точки зрения мы получили исходный непрерывный сигнал x(t).

3.5. Погрешности      дискретизации     и    восстановления

                                непрерывных    сигналов.

Теорема Котельникова точно справедлива только для сигналов с финитным (конечным) спектром. На рис.3.14 показаны некоторые варианты финитных спектров:

                                 S_x(w)         3

                                        2                                                     

                                                 1

                             0                          w_в                                   w        

                                                              Рис.3.14.

Однако спектры реальных информационных сигналов бесконечны. В этом случае теорема Котельникова справедлива с погрешностью.

                                 S_x(w)   

                                                                               

                             0                          w_в                                   w

              Рис.3.15.

Погрешность дискретизации определяется энергией спектральных составляющих сигнала, лежащих за пределами частоты w_в.

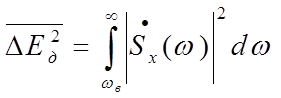                                                                    (3.7)

 Вторая причина возникновения погрешностей - неидеальность восстанавливающего ФНЧ.

Т.о. погрешность дискретизации и восстановления непрерывного сигнала определяется следующими причинами:

1)  Спектры реальных сигналов не финитны.