Теория электрической связи: Конспект лекций. Часть 1, страница 6

Любая непрерывная функция, спектр которой не содержит частот

выше  , полностью определяется своими отсчетами, взятыми через интервал времени 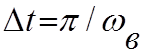.  ( Теорема Котельникова)

Временные диаграммы непрерывного сигнала x(t)  и дискретизированного  x _д(t) имеют вид:

            x(t)

                                                             t

                      0      Dt     2Dt    3Dt    4Dt                      Рис. 3.1

          x_д(t)

 

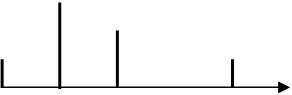                      0      Dt     2Dt    3Dt    4Dt     t

       Важно, что не надо передавать       непрерывно исходный сигнал x(t),

достаточно передавать отсчёты  x(kDt).           Это первый шаг перехода от

непрерывного сигнала к цифровому.  С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:

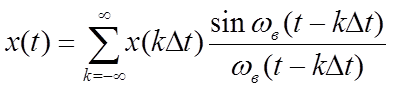                                          (3.1)

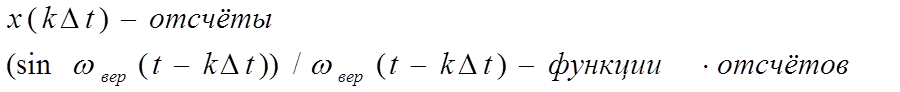      Ряд Котельникова – это разложение сигнала  в ряд по ортого-

нальным функциям .

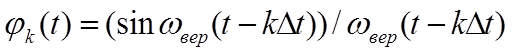                        (3.2)   

      Теоретически дискретизация осуществляется с помощью  d-импульсов .  Временная диаграмма одиночного d- импульса имеет вид:

                                             u(t)

                                                       

                                                                d(t-a)                                                                                                 

            Рис. 3.2                         0        a                                        t                                   

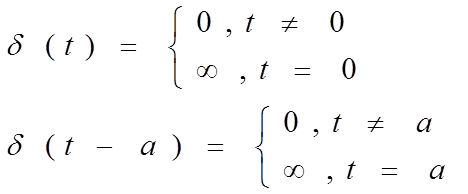
Спектр одиночного - импульса получим, используя преобразование  Фурье:

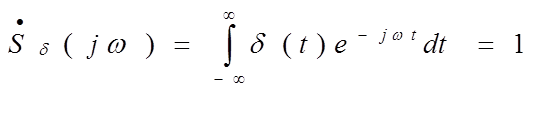
 Использовано

 "фильтрующее" свойство дельта-функций:

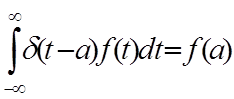 Следовательно, спектр одиночного дельта-импульса  имеет вид:                              

                                                     S(jw)

                                                 1

 

                                                                                                 Рис. 3.3

                                                                              w

Чтобы получить отсчёты функции перемножим функцию  на периодическую последовательность - импульсов с периодом Т=Dt. Временная диаграмма периодической последовательности дельта-импульсов имеет вид:

                                                                                u_d(t)

               d(t+4Dt) d(t+3Dt)   d(t+2Dt)  d(t+Dt)       d(t)  d(t-Dt)   d(t-2Dt)   d(t-3Dt)

 

            . . .                                                                                     . . . .

 

              -4Dt    -3Dt    -2Dt     -Dt       0       Dt      2Dt     3Dt     4Dt           t

                                                                            Рис.3.4

Так как сигнал периодический, то его спектр будет        дискретным.

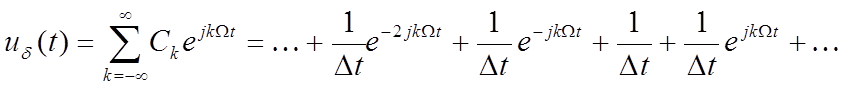
                                                                                                                                                       (3.3)

    ;         

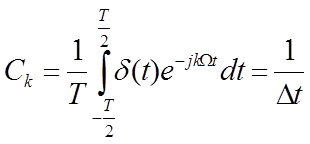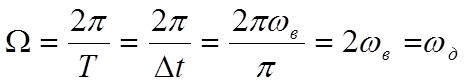
            Т =D t     ;                            -частота дискретизации.

Спектр периодической последовательности - импульсов в соответствии с формулой  для U(t) имеет следующий вид :

                                                                              S(jw)     

                                                                              1/Dt                                                Рис.3.5

                  . . . . . .                                                                                                  . . . . .

                                                                                                                                                        t