Теория электрической связи: Конспект лекций. Часть 1, страница 23

Огибающая нормального случайного процесса Um(t)  распределена по закону Релея:

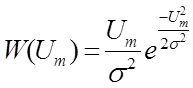;  U_m  ³ 0

           W(Um)  

 

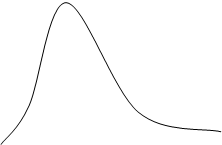
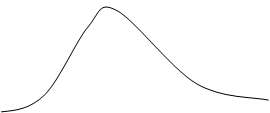                                     з-н Релея

                                                           з-н Райса                         Рис.11.10.

 

                     0                                                               Um

Если узкополосный случайный процесс есть сумма нормального шума и гармонического колебания с амплитудой А, то его огибающая распределена по обобщенному закону Релея (закон Райса):

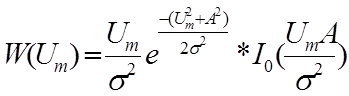    закон Райса.

I₀(.) - функция Бесселя от мнимого аргумента.

11.6.ФПВ и ФРВ для дискретных случайных  процессов.

Дискретные случайные процессы принимают с определенной вероятностью значения, отличающиеся одно от другого на конечную величину. Вероятность таких значений – число не равное 0.

Рассмотрим реализацию дискретного случайного процесса.

               x(t)

                   а            

                          T₁

                           

Т₂                                            t            Рис.11.11

                   b                              

                                              T₁+T₂=T

Для эргодического стационарного случайного процесса усреднение по множеству реализаций эквивалентно  усреднению по времени одной реализации.

 

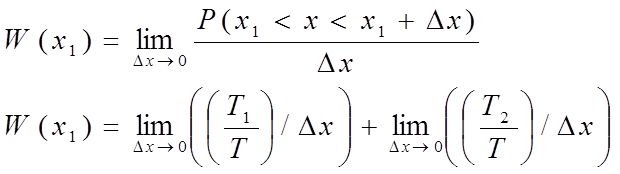
T₁/T- вероятность того, что случайный процесс принимает

        значение а.

T₂/T - вероятность того, что случайный процесс принимает

        значение b.

ФПВ заданного случайного процесса в соответствии с полученным выражением показана на рис.11.12:

                                                    W(x)

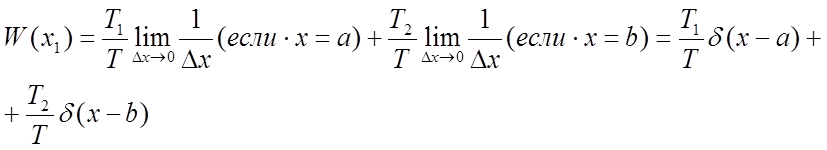
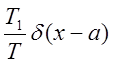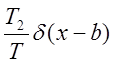Рис.11.12.

                                           b      0          a               x                                                                                                                 

                        

ФРВ для случайного процесса принимающего 2 значения x=a  и x=b  имеет вид:

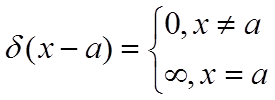
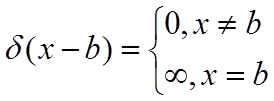
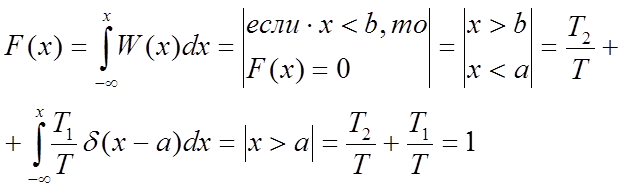
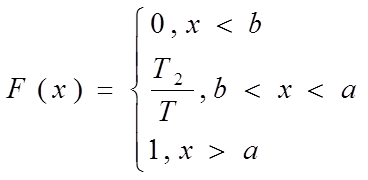
                                                       F(x)

                                                  1

                                 T₂/T₁

                                                                                         Рис.11.13.

                                                         t

                                      b                           a

Вычислим среднее значение двоичного дискретного случайного процесса, принимающего 2 значения:

x=ac  вероятностью T₁/T, x=bc вероятностью T₂/T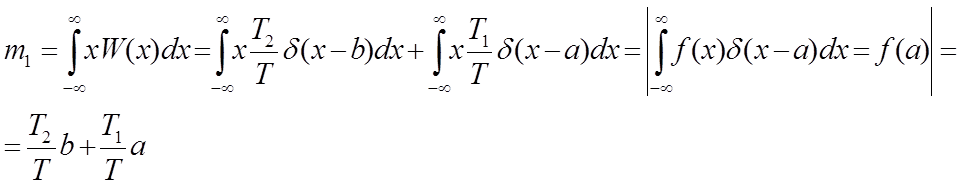

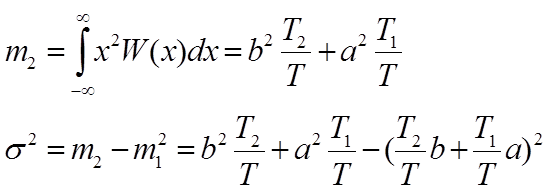
11.7.Нелинейные безынерционные преобразования случайного процесса.

    Нелинейное преобразование:

    y(t)=f[x(t)] – называется безынерционным, если y(t_k) в момент времени t_kзависит только от x(t_k).

ФПВ для процесса yна выходе:

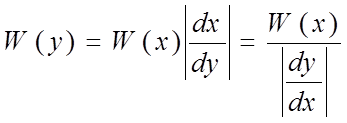
Пусть характеристика нелинейного элемента может быть аппроксимирована линейно-ломаными.

                                                              y

                                                                                  Рис.11.14

                                                          b

                                               -a                    a                         x

-b

                                                               

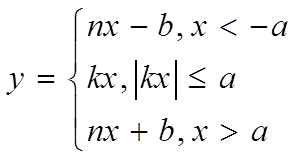
Это нелинейное устройство называется ограничителем.

Пусть на входе ограничителя действует нормальный случайный процесс с нулевым средним m_1x=0.

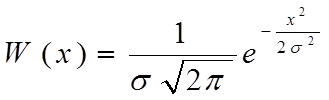
ФПВ   процесса x нарисована на рис.11.15 (верхний рисунок).

Рассчитаем  ФПВ процесса y:

1. Пусть      у=kx (k>1)

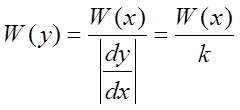                                                                                                 Подставим в W(x) вместо x, y/k, тогда

  

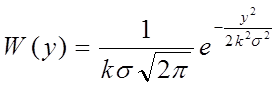
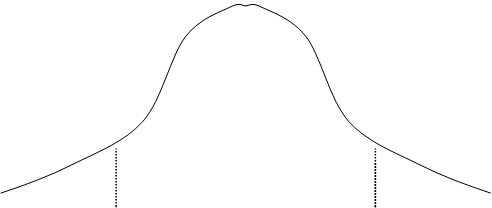
На интервале  ФПВ для у будет нормальной, со средним значением m_1y=0, но дисперсия y, т.е. .

                                                             W(x)