Теория электрической связи: Конспект лекций. Часть 1, страница 5

то этот ряд (2.1)  называется  рядом Фурье.

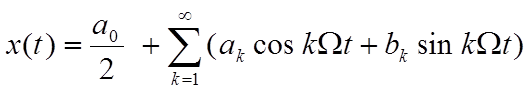
                               (2.2)

 

      _;                  

 

 

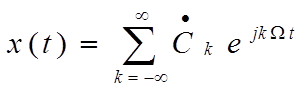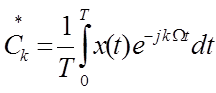
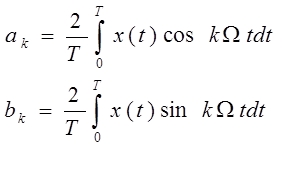
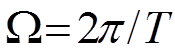
 - частота первой гармоники, определяемая     периодом T

  (  T- период функции  x(t) ).

Разложение сигнала в ряд Фурье называется  спектром сигнала.

Спектр периодического сигнала – дискретный.

Спектр непрерывного сигнала – сплошной и определяется интег-

ралом Фурье:               -¥

                     S(jw) =   ò x(t)e ^-jwt  dt                                               (2.3)

                               - ¥

Шириной спектра сигнала Пэназывается полоса частот, в пределах которой заключена основная доля энергии сигнала.

В качестве примера  рассчитаем спектр периодической последовательности прямоугольных импульсов c амплитудой  А:

    x(t)

          А

                                                           .  .  .  .           Рис.2.1

            t           T                                                 t

Определим коэффициенты разложения в ряд Фурье C_к :

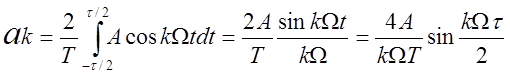                t/2

b_k = 2/Т ò A sin kWt dt = 0, т.к. подинтегральная функция - нечетная.

            -t/2

Пусть Т = 2t, тогда коэффициенты a_k равны:

   a₀ = А,      a_k = 2А/ kp (sin kp/2), при к > 0.

Итак, временная диаграмма периодической  последовательности импульсов показана на рис.2.1. Спектр этой последовательности  показан на рис.2.2.

       a_k

                    2A/p

  A/2

                                              2A/3p                                    Рис.2.2.

 

                                        .                           .

          0            W            2W         3W        4W         w

Ширина спектра сигнала равна, в данном случае, Пэ =2p/t.

 Спектр непериодического сигнала ( спектральная плотность) , как уже сказано выше, может быть получен с помощью интеграла Фурье. Для одиночного прямоугольного импульса с амплитудой А и длительностью t  на рис.2.3  получим спектр S(jw) на рис.2.4 :

  

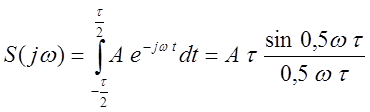                                                        S(jw)

           

            x(t)

                        А                                   

                                                        

                  t                     t           0                                                    w

                                                             2p/t      4p/t

         Рис.2.3.                                         Рис.2.4.

 Спектр непериодического сигнала сплошной, бесконечный, ширина спектра определяется длительностью сигнала  и, ориентировочно, равна  Пэ =2p/t.

                          Вопросы   для  самопроверки

1.  Какие функции называются  ортогональными?

2.  Запишите  ряд Фурье в общем виде.

3.  Что такое спектр сигнала?

4.  Запишите выражение для спектра периодического сигнала.

5.  Рассчитайте амплитуды гармонических составляющих  для периодической последовательности прямоугольных импульсов.

6.  Что такое ширина спектра сигнала?

7.  Чему равна ширина спектра последовательности  импульсов?

8.  Запишите выражение для спектра непериодического сигнала.

9.  Рассчитайте и постройте спектр одиночного прямоугольного импульса.

10. Какие параметры  сигнала влияют на ширину спектра и на частоту гармонических составляющих спектра?

3.Теорема Котельникова.

3.1.Разложение непрерывных  сигналов в ряд Котельникова

Телекоммуникационные сигналы делятся на непрерывные и дискретные.

Непрерывные сигналы (функции) могут принимать любые , сколь угодно близкие друг к другу значения, в любые моменты времени. Примером непрерывного сигнала является гармоническое колебание.

Дискретные (цифровые) сигналы могут принимать только заранее известные значения, отличающиеся одно от другого на конечную величину, причем изменяться эти значения могут только в определенные моменты времени. Примером дискретного сигнала является (см. рис.2.1 ) периодическая последовательность прямоугольных импульсов, которая в моменты времени  ( -t/2 +кТ ) принимает значения или 0, или А.