Теория электрической связи: Конспект лекций. Часть 1, страница 24

                                                                        x            

                                      -a                                   a

 

                                                 W(y)

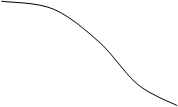                                                                                                     Рис.11.15.

 

                               -ka                     0                        ka                  y

2. Пусть:

                 

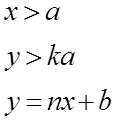
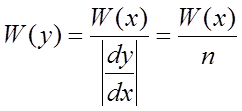
Выражаем xчерез у, т.е.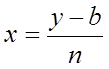

 

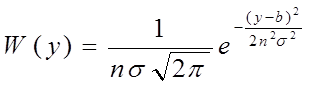
 Это нормальная ФПВ со средним значением b и дисперсией

3.Пусть:  

                                                                                                                                                                                                                               

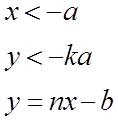
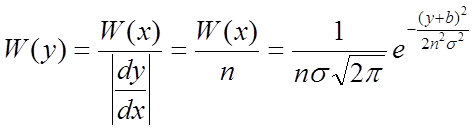
Это нормальная ФПВ, m₁= -b и дисперсия .

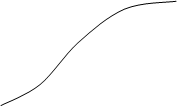
ФПВ процесса y дана на рис.11.15 (нижний рисунок).

11.8.ФПВ процесса на выходе идеализированного ограничителя.

Такой ограничитель имеет горизонтальные участки насыщения.

 

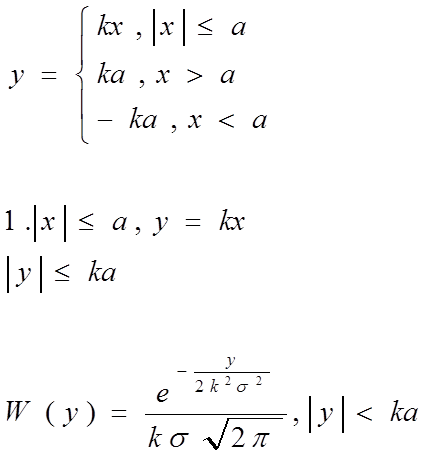
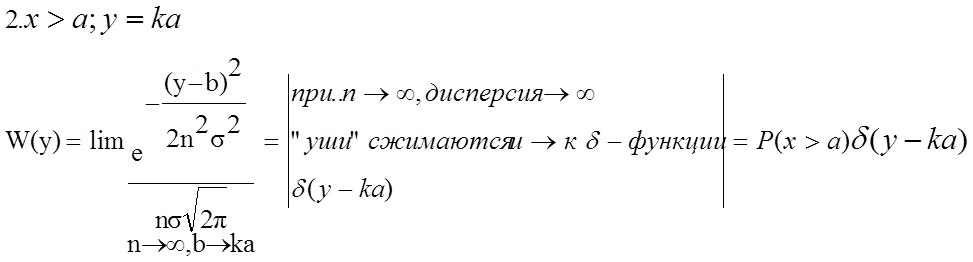
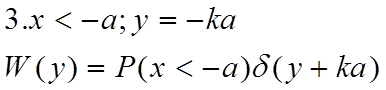
                                                 W(y)

                 P(x<-a)d(y+ka)                                   P(x>a)d(y-ka)

                                                                                                     Рис.11.16.

 

                               -ka                     0                        ka                  y

11.9.ФПВ процесса на выходе идеального ограничителя.

Характеристика  идеального ограничителя показана на рис.11.17.

y

                                                     ka                                          Рис.11.17.

x

-ka

 

 Процесс  на выходе  идеального ограничителя   y - имеет только два значения : ка и –ка.  Т.к. вероятность положительных и отрицательных значений х  равна 0.5, то вероятность того, что y принимает значения +ka или -ka также равна 0.5. Поэтому, выполняя расчеты, как в предыдущем случае, получим, что ФПВ процесса y  вырождается в две дельта-функции в точках y=-ka и y=ka (рис.11.18):

                                                 W(y)

                          0,5 d(y+ka)                                   0,5 d(y-ka)

                                                                                                     Рис.11.18.

                               -ka                     0                        ka                  y

11.10.Линейные (инерционные) преобразования случайного процесса.

Линейная инерционная система – это линейный фильтр.

В этом случае процесс на выходе системы у(t1) зависит от входного процесса x не только в момент времени t1, но и от значений x в  предшествующие  и последующие моменты времени:

1.  Если процесс на входе ЛЭЦ нормальный, то у тоже нормальный случайный процесс, но его числовые характеристики отличаются от числовых характеристик процесса x и вычисляются следующим образом:

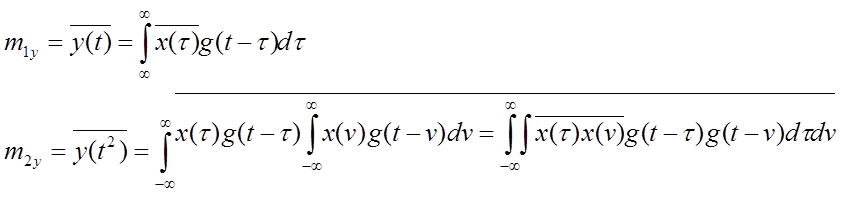2. Если процесс на входе ЛЭЦ не нормальный, но ширина его спектра значительно больше полосы пропускания линейной цепи , то процесс на выходе ЛЭЦ имеет тенденцию к нормализации.

Вопросы для самопроверки.

1.  Какой процесс называется случайным?

2.  Что такое ФПВ и ФРВ?  Как они связаны?

3.  Запишите выражения для числовых характеристик случайного процесса.

4.  Какой процесс называется нормальным?

5.  Постройте ФПВ для произвольного двоичного случайного процесса.

6.  Какой процесс называется узкополосным?

7.  Запишите выражение для ФПВ процесса на выходе нелинейной цепи.

12.Функция корреляции.

Функция корреляции характеризует степень статистической зависимости двух  значений случайного процесса, разделенных интервалом времени t.

Общее определение – функция   корреляции      случайного  процесса

 B(t1,t2) это второй центральный  смешанный момент распределения случайного процесса.