Теория электрической связи: Конспект лекций. Часть 1, страница 22

 

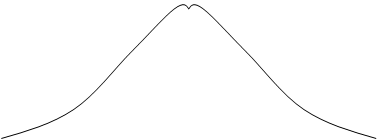
                                                                                                     Рис.11.3.

 

                                          3s                      3s                   x

Если известна дисперсия и m₁, то рабочий участок ВАХ должен иметь протяженность m₁±3s.

8. ФРВ для нормального случайного процесса

    

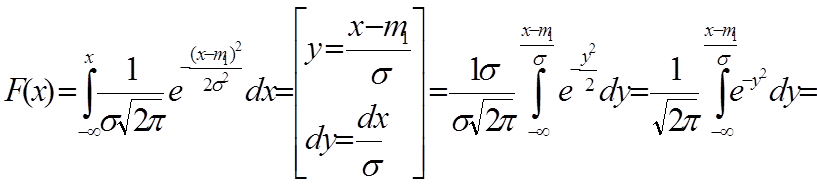
 = F(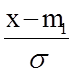)    - табулированная функция (интеграл вероятности Лапласа)

F (0)  =  0.5                                              F (-x)  =  1- F(x)

F(3.9)  =  0.99995                                   F (-¥)  =  0; F(¥)  =  1.

ФРВдля нормального процесса имеет вид:

             F(x)

                   1

                0.5                                                               Рис.11.4.

                     0                   m₁                                       x

11.3.ФПВ и ФРВ для  гармонического  колебания со  случайной  начальной фазой.

 Рассмотрим случайный процесс в виде гармонического колебания со  случайной  начальной фазой:

            X(t) = Asin ( wt + j )

 j - случайная величина, равномерно распределенная на интервале   ± p, т.е. ФПВ мгновенных значений фазы , показанная на рис.11.5 равна:

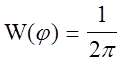   ;  |x| £ p

                                              W(j)

                                    1/2p

 

                                                                                      Рис.11.5.

                             -p           0        p                 j

Вычислим среднее значение j:

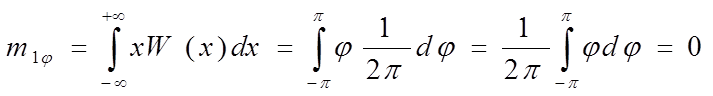
Вычислим дисперсию:

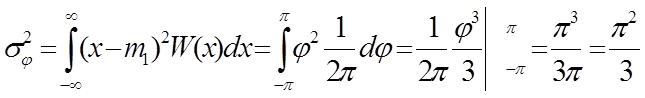
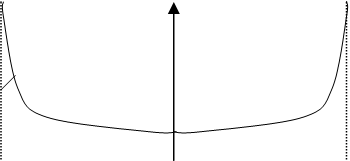
ФПВ мгновенных значений x гармонического колебания со случайной фазой, изображенная на рис. 11.6, имеет вид:

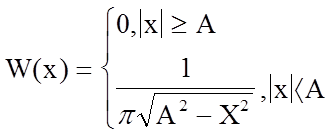
W(x)

 

                                                                              Рис.11.6.

 

-A                      0                      A          x

Чем больше А, тем кривая ниже и шире. Заштрихованная площадь равна единице. Это площадь под кривой W(x) (условие нормировки)..

ФРВ мгновенных значений для гармонического колебания со случайной фазой:

X(t) = Asin ( wt + j )

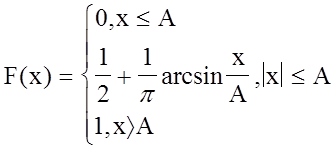
F(x)

                                                         1

                                                      0.5

                                                                                   Рис.11.7.

 

                                    -A                  0                  A               x

11.4.ФПВ для суммы нормального случайного процесса и гармонического колебания со случайной начальной фазой.

Рассмотрим случайный процесс z(t), равный:

Z(t) = x(t) + Asin (wt+ j)

где x(t) - нормальный случайный процесс;

      Asin (wt+ j) - гармоническое колебание со случайной начальной фазой.

W(z) в этом случае находится сверткой.

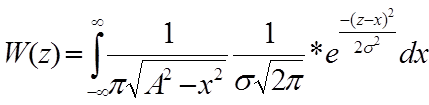
Вид ФПВ, т.е. W(z) зависит от параметра:

 

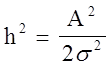
    W(z)

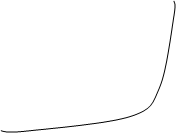
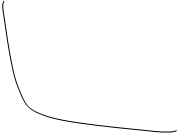                              h²=0                 h²=¥

 

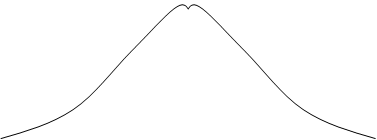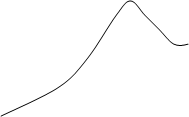
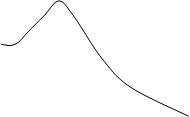                      h²= 6

                                                                         Рис.10.8.

                                    0                                     z

h² = 0  -  нормальный случайный процесс    (чистый шум).

h²  ® ¥  -  одно гармоническое колебание.

11.5.Огибающая и фаза узкополосного случайного процесса.

Случайный процесс y(t) = U_m(t) cos ( w₀t+j(t) ) называется узкополосным, если его ширина спектра значительно меньше, чем средняя частота w₀.

U_m(t) - огибающая случайного процесса (случайная амплитуда) на  рис.11.9;

j(t) - фаза случайного процесса.

Для нормального случайного процесса  фаза j(t) распределена равномерно (см. выше).

             u(t)                       Um(t)

                                                                          Рис.11.9.

 

                                                                t