Функция распределения вероятностей обозначается F(x), характеризует вероятность того, что случайный процесс в некоторый момент времени t1 принимает значение меньшее x1 . Полное обозначение одномерной ФРВ
F(x1 ,t1 ) = P(x<x1 , t=t1 )
Двумерная ФРВ.
F2 (x1 t1 ,x2t2) = P (x<x1, t=t1 ,x<x2;t=t2)
Наиболее полная характеристика n- мерная ФРВ:
Fn (x1t1...xntn) = P (x<x1;t<t1; ... x<xn;t=tn)t
Функция плотности вероятностей случайного процесса ( ФПВ)
В простейшем случае одномерная ФПВ равна:
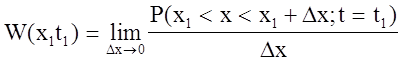
Одномерная ФПВ равна пределу отношения вероятности попадания случайного процесса в интервал от x1 до х1+Dх, при t= t1, к Dх при Dх стремящемся к нулю.
Наиболее полной характеристикой является n - мерная ФПВ.
ФРВ и ФПВ связаны друг с другом . ФПВ - это первая производная ФРВ по х1, Соответственно, ФРВ равна интегралу от -¥ до х1 от ФПВ:.
:
F(x1t1) =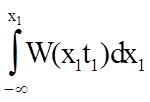 
Условие нормировки :
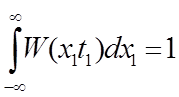
Числовые характеристики случайного процесса .
Среднее значение ( математическое ожидание или первый начальный момент)
m1 =`x =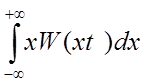 
Физический смысл m1 - это постоянная составляющая случайного процесса.
2.Второй начальный момент.
m2 = `x2 =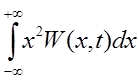 
Физический смысл m2 - это полная средняя мощность случайного процесса на единичном сопротивлении.
3.Дисперсия ( второй центральный момент )
s2 = М2
= 
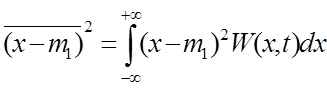
Физический смысл s2 - это средняя мощность переменной составляющей случайного процесса на единичном сопротивлении.
Числовые характеристики связаны между собой:
s2 = m2 - m12
Стационарность.
1. Нестационарный случайный процесс - ФПВ и ФРВ зависят от начала отсчета времени.
2. Стационарный в узком смысле - ФПВ и ФРВ не зависят от начала отсчета времени.
3. Стационарный в широком смысле - одно- и двумерные ФПВ и ФРВ не зависят от начала отсчета времени.
Для стационарного случайного процесса m1, m2, s2 - не зависят от времени.
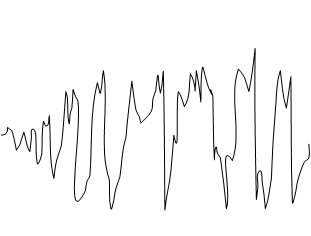Рассмотрим тепловой шум на выходе включенного усилителя:
x(t)
Рис.11.1.
t
нестационарный Стационарный
После включения усилитель прогревается и шум на его выходе - нестационарный. После "прогрева" шум будет стационарным процессом.
Эргодичность.
Случайный процесс называется эргодическим, если для него усреднение по времени одной реализации и усреднение по множеству реализаций дает один и тот же результат. Это свойство имеет большое значение на практике, т.к. усреднение по времени одной реализации технически реализовать проще, но оно не всегда дает истинный результат. Поэтому доказательство эргодичности процесса позволяет существенно упростить нахождение его характеристик.
11.2.Нормальный случайный процесс( гауссов процесс).
Процесс называется нормальным или гауссовым, если его одномерная ФПВ имеет вид:
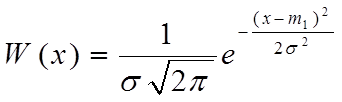
Графики нормальной ФПВ построены на рис. 11.2.:
W(x)
s1
s1 s1
m1<0 m1=0
m1>0 Рис.11.2.
s2>s1
 |
m1 - среднее значение случайного процесса . x
s2 - дисперсия случайного процесса .
Свойства нормального случайного процесса .
1. W(x) ³ 0
2. Нормальная ФПВ симметрична относительно x = m1
3. W(x) - max при х = m1
4. Площадь под кривой W(x) равна 1.
5. При изменении m1 форма кривой не меняется, но кривая смещается вдоль оси х.
6. Чем больше дисперсия s2, тем кривая ниже и шире.
7. С вероятностью близкой к 1 (Р@0,997) мгновенные значения нормального случайного процесса лежат в пределах:
m1 - 3s < x < m1+3s
W(x)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.