Теория электрической связи: Конспект лекций. Часть 1, страница 26

Рис.14.2.

                                                      0                                 t

 Рассмотрим прохождение белого шума через полосовой фильтр. На входе идеального полосового фильтра с АЧХ равной :

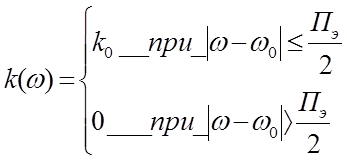
действует нормальный белый шум со спектральной плотностью G₀. Определим функцию корреляции и ФПВ процесса y на выходе фильтра; т.е. В(t)_вых  и  W(y) .

Спектр белого шума на входе фильтра показан на рис.14.1.

АЧХ полосового фильтра показана на рис. 14.2, а спектр процесса на выходе полосового фильтра изображен на рис.14.3. 

                 К(w)  

           К0

             0       (w0 -Пэ/2)     w0       (w0 +Пэ/2)      w

                                                                 Рис.14.2

  G(w)вых

G0К0²

             0       (w0 -Пэ/2)     w0       (w0 +Пэ/2)      w

                                                               Рис.14.3.

Спектральная плотность  белого шума на выходе ПФ: G(w)_вых = G₀К₀², т.к. АЧХ показывает во сколько раз изменится амплитуда напряжения, следовательно, энергия изменится в К₀² раз. В соответствии с соотношением Винера - Хинчина, зная G(w)_вых найдем В(t)_вых. :

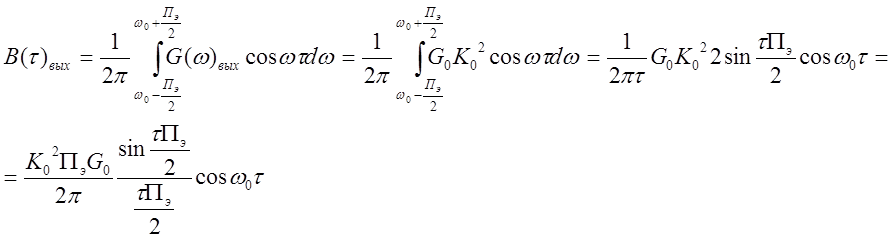
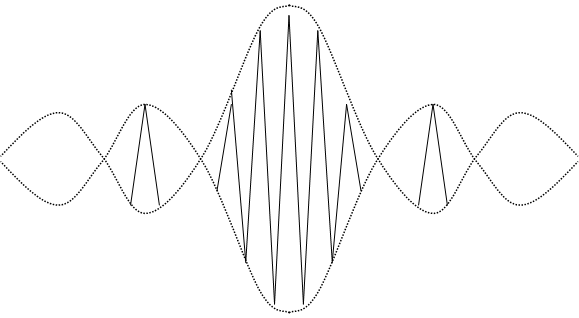
График функции корреляции процесса на выходе ПФ показан на рис.14.4:

                                                       В(t)_вых

                                                                                                        Рис.14.4.

 

                                                                                                   t

                                  -2p/Пэ                    2p/Пэ

Определим ФПВ процесса у на выходе фильтра.

Т.к. процесс на входе фильтра нормальный с нулевым средним значением, то процесс y на выходе фильтра  тоже будет гаусовским процессом с нулевым средним значением и дисперсией s², которая равна Bвых(0), как это указывалось в разделе , посвященном  изучению функции корреляции:

                    

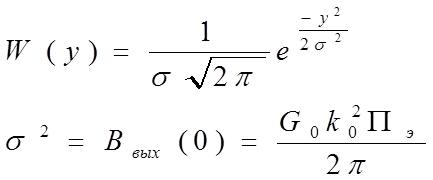
Анализ графика  функции корреляции на рис.14.4 позволяет определить интервал корреляции для  процесса на выходе фильтра. Интервал корреляции вычисляется  в данном случае  как расстояние от точки t =0 до значения t, при котором функция корреляции первый раз обращается в ноль. Из графика следует, что интервал корреляции равен  2p/п_э, т.е. обратно пропорционален ширине спектра процесса.

Вопросы для самопроверки.

1.Рассчитайте функцию корреляции случайного процесса , если  известен его энергетический спектр.

2.Рассчитайте энергетический спектр процесса, если известна его корреляционная функция

3. Что такое белый шум?

4. Определите функцию корреляции случайного процесса  на выходе полосового фильтра, если на входе фильтра действует белый щум.

15. Модели непрерывных   каналов связи.

Реальные каналы связи  достаточно сложно  описать  таким образом, чтобы удовлетворить требования разработчиков телекоммуникационной аппаратуры  и  специалистов, занимающихся эксплуатацией  систем связи.  В то же время   при  решении практических задач   некоторые параметры канала связи  являются несущественными для  одного класса задач,  и  определяющими для другого. Поэтому были   разработаны  несколько моделей, которые отражают наиболее существенные параметры и характеристики типичных  реальных каналов связи:

Идеальный канал без помех

   Сигнал на выходе такого канала   определяется так:

                           s(t) = k u(t - t),

     где  s(t) - сигнал на выходе канала,

             u(t) - сигнал на входе канала,

             k - коэффициент передачи канала,

             t - время задержки сигнала в канале.

     Параметры канала - постоянны.

Канал с аддитивным гауссовским шумом

 Сигнал на выходе такого канала имеет  вид:

                      s(t) = k u(t - t) + x(t),

                где  x(t) - нормальный шум.

   Параметры канала либо постоянны, либо являются известными    функциями времени.