Работа при перемещении электрического заряда. Движение заряженной частицы в однородном электрическом поле, вакууме; движение потока частиц; сила тока; плотность тока. Ток в металлах. Закон Ома для замкнутой цепи. Законы Кирхгофа. Виды соединения проводников, страница 9

.

 где q - заряд (в СИ измеряется в кулонах, Кл);

       Е - напряженность электрического поля.

Количественной характеристикой этого процесса является сила тока

Из электростатики нам известно, что в электрическом поле положительные заряды будут двигаться от большего потенциала к меньшему. Таким образом, для того, чтобы в цепи протекал электрический ток, на концах проводника необходимо поддерживать разность потенциалов (напряжение), не равную нулю.

Электрическое поле неподвижных электрических за­рядов - электростатическое поле - обладает одним весь­ма характерным свойством: работа при перемещении электрического заряда из одной точки такого поля в другую не зависит от того, по какой траектории происхо­дит перемещение заряда, а определяется лишь положением этих точек.

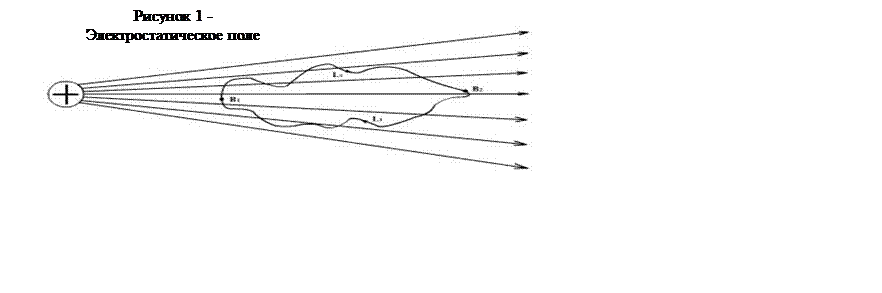Допустим, что работа поля А₁ по перемещению заря­да q₁ вдоль траектории ℓ₁ больше работы А₂ вдоль траек­тории ℓ₂ (рисунок 1). Если заряд q сначала перемещается за счет действия на него поля из точки В₁ в точку В₂ вдоль траектории ℓ₁ а затем внешней силой возвращается в точку В₁ вдоль траектории ℓ₂, то в результате такого перемещения заряда по замкнутому контуру получился бы выигрыш в работе:

.

 Но после возвращения заряда q в исходное положе­ние восстанавливается первоначальное состояние систе­мы и, следовательно, исходное значение ее энер­гии. Значит, выигрыша в работе не должно быть, т. е. А=0 и

т. е. работа при перемещении заряда между двумя точка­ми в электростатическом поле не зависит от формы тра­ектории, а определяется лишь положением этих то­чек.

 Полученный вывод может быть сформулирован еще и так: работа электростатического поля при переме­щении заряда по любому замкнутому контуру равна нулю.

Поля, работа которых не зависит от формы траекто­рии, а зависит лишь от начального и конечного положе­ния заряда в поле, называют потенциальными полями. Следовательно, электростатическое поле – поле потен­циальное.

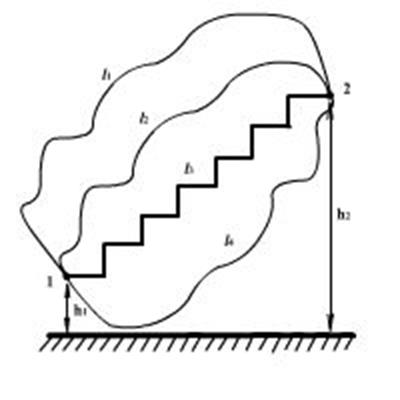Ранее вы уже встречались с потенциальным полем: потенциальным полем является гравитационное поле, так как совершаемая им работа зависит лишь от началь­ного и конечного положения тела (рисунок 2).

.

Разность потенциалов

Мы уже знаем, что работа электростатического поля при перемещении заряда не зависит от формы траекто­рии и определяется лишь положением начальной и ко­нечной точек этой траектории.

Сила, с которой поле действует на заряд F=qE, прямо пропорциональна заряду. Поэтому и работа, со­вершаемая полем при перемещении заряда, будет также прямо пропорциональна заряду. Следовательно, отноше­ние этой работы к заряду не зависит от заряда; не зависит оно и от траектории, по которой происходит перемещение заряда. Это отношение зависит лишь от самого поля и выбора исходной и конечной точки пере­мещения заряда в нем.

Величина, равная отношению работы, совершенной полем при перемещении заряда, к этому заряду, полу­чила название разности потенциалов.

.

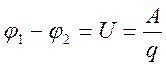Здесь индексы 1 и 2 обозначают точки, между кото­рыми перемещается пробный заряд q.

Таким образом, разностью потенциалов называют скалярную величину, являющуюся энергетической харак­теристикой электростатического поля. Разность потен­циалов равна отношению работы, которую совершает поле при перемещении положительного заряда между двумя точками поля, к этому заряду.

За единицу разности потенциалов в Международной системе единиц принимается вольт (1 В). Разность потенциалов равна 1 В, если при перемещении между двумя точками заряда в 1 Кл поле совершает работу в 1 Дж:

.

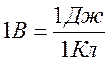Измерение разности потенциалов

Для измерения разности потенциалов созданы специальные приборы - электростатические вольтметры Знакомый вам электрометр является таким прибором. Для измерения разности потенциалов стержень электрометра присоединяют к одной точке, а корпус - к другой точке поля. Между стержнем и корпусом возникает электрическое поле (рисунок 3), которое действует на каждый элемент заряженной стрелки с силой, пропорциональной напряженности поля в этой области и, следовательно, разности потенциалов.