Работа при перемещении электрического заряда. Движение заряженной частицы в однородном электрическом поле, вакууме; движение потока частиц; сила тока; плотность тока. Ток в металлах. Закон Ома для замкнутой цепи. Законы Кирхгофа. Виды соединения проводников, страница 6

A₁₂ = Q×E×d₁+...+Q×E×d_n. = Q×E×(d₁+d₂+.. .+d_n.) = Q×E×d₁₂

В то же время

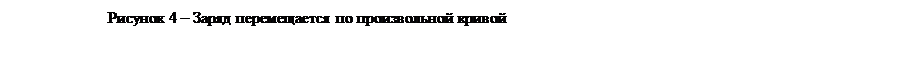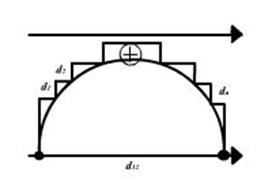
Работа электрических сил не зависит от формы траектории. В однородном поле между напряжённостью и разностью потенциалов существует связь.

·  Иногда приходится рассматривать работу при .

А_замкн=0.

Работа кулоновских сил на замкнутом пути всегда равна нулю.

Понятие напряженности и электродвижущей силе

Вернёмся к полной работе при перемещении заряженного тела в пространстве.

Найдём работу, приходящуюся на единицу заряда.

A/Q = A_кул/Q + Aстор/Q

Принято называть: A/Q = U напряжением;

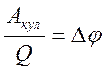 - разность потенциалов;

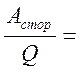 ε - электродвижущей силой.

А = 1 Дж, Q = 1Кл, U = 1 Дж/Кл = 1В.

Напряжение, разность потенциалов и ЭДС измеряются одной и той же единицей - вольтом (В).

В тех случаях, когда ЭДС отсутствует, то различие между напряжением и разностью потенциалов исчезает, т.е.

, при .

Движение заряженной частицы в однородном электрическом поле, в вакууме

Если заряженная частица находится в электрическом поле, то её взаимодействие с полем характеризуется силой F = Q×E и энергией W = Q×φ.

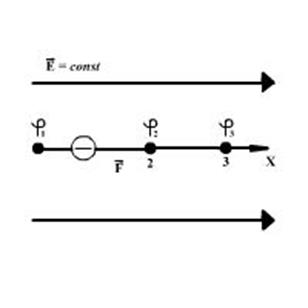
При постоянной напряженности сила тоже остается постоянной. Под действием этой силы частица будет двигаться равноускоренно. X = Q×t²/2; υ = Q×t; a = Q×E/m; Wk = m×υ²/2

По закону сохранения энергии

.

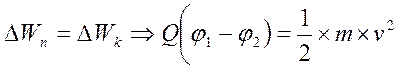Кинетическая энергия с увеличением скорости возрастает, а потенциальная будет уменьшаться, значит φ₁ >φ₂ >φ₃. Потенциалы точек, через которые проходит частица, постепенно уменьшаются. Под действием кулоновских сил положительно заряженная частица всегда движется от точек с большим потенциалом.

Движение потока заряженных частиц в электрическом поле, в вакууме. Сила тока. Плотность тока.

Допустим, в однородном электрическом поле движется не одна, а множество заряженных частиц. Под действием электрического поля частицы придут в направленное движение, причем каждой отдельной частицы происходит так, как мы говорим только что.

Направленное движение множества заряженных частиц называют электрическим током. Для характеристики электрического тока вводят понятие силы тока и плотность тока.

Сила тока определяется зарядом, прошедшим через площадь поперечного сечения проводника за одну секунду.

I = Q/t,

где I - сила тока

 Q - заряд

  t - время

Сила тока измеряется Амперами, причем 1А - основная единица СИ.

Плотность тока определяется силой тока, проходящей через площадь 1м²,

J = I/S   j – плотность тока

I=1A; S = 1м²; j = 1A/м²

Сила и плотность тока можно вычислить через концентрацию частиц и скорость их движения.

Допустим, что частицы движутся вдоль силовых линий электрического поля с некоторой средней скоростью v.

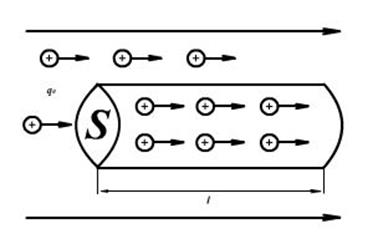
I = Q/t, Q = N*q_o, где N - число частиц прошедших через сечение S за время t, a q_o – заряд одной частицы.

I = Nq_o/S

За время t через сечение S пройдут все частицы, которые окажутся, внутри цилиндра, площадь которого S, а длина

1 =v×t;

V = S×v×t.

Если в единице объёма содержится n частиц, то г = n×v = n×S×v×t

I = n×S×v×t×q_o/t = q_o×n×v×S, a j = q_o×n×v

Сила тока в цепи     I = q_o×n×v×S

Плотность тока        j = q_o×n×v

Ток в металлах, понятие о классической теории электропроводимости металлов

Металлы являются хорошими проводниками и как проводники они получили большое распространение. Любая электрическая цепь содержит металлические проводники.

Основные положения теории электропроводимости металлов:

1 Проводимость металлов обусловлено наличием в них свободных электронов.

2 Концентрация свободных электронов в металлах очень велика и составляет n ≈ 1029 электронов в 1м³, n алюминия = 2.08×10²⁹м^-3, n меди=1.14×10²⁹м^-3

3 Концентрация свободных электронов не зависит от температуры и других внешних условий.

4 Свободные электроны ведут себя подобно идеальному газу, следовательно, к ним можно применить законы идеального газа.

5 Свободные электроны движутся хаотически. Скорость хаотического движения зависит от температуры .