Значит, измеряя напряжение на полюсах источника, замкнутого внешней нагрузкой, сопротивление которой R ›› r, мы получаем приближенное значение ЭДС источника. Чем больше сопротивление внешней нагрузки по сравнению с внутренним сопротивлением источника, тем более точный результат будет получен. Очевидно, что ЭДС равняется напряжению между полюсами разомкнутого источника тока (когда сопротивление внешней цепи бесконечно велико).
Короткое замыкание
Какие же предельные значения силы тока можно получить в цепи, пользуясь данным источником тока? ЭДС источника ε и его внутреннее сопротивление rявляются величинами постоянными. Поэтому сила тока в цепи будет зависеть только от сопротивления внешней цепи R.
Пусть к полюсам источника присоединили проводник, сопротивление которого ничтожно мало по сравнению с внутренним сопротивлением источника. Этот случай получил название короткого замыкания.
Из закона Ома следует, что если сопротивление R=0, то напряжение между полюсами источника (U = IRуменьшается до нуля, а сила тока короткого замыкания достигает максимального значения:
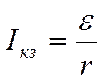 .
.
Как мы видим, сила тока короткого замыкания зависит не только ЭДС источника, но и от внутреннего сопротивления. У источника сравнительно большим внутренним coпротивлением, как, например, у клинических элементов, сила тока короткого замыкания небольшая, а потомэтот ток для них не очень опасен.
Иное дело в свинцовых аккумуляторах внутреннее сопротивление их мало (0,1 0,01 Ом). Поэтому сила тока короткого замыкания очень велика, порядка 20-200 А. Такой ток может разрушить пластины аккумуляторов. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций. При значительной ЭДС (свыше 100 В) внутреннее сопротивление этих источников ничтожно мало.
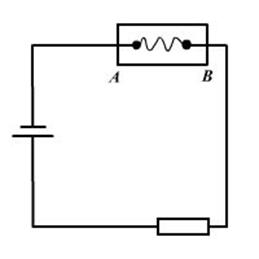
Рисунок 3 – электрическая цепь с предохранителем
Поэтому сила тока короткого замыкания может достигнуть тысяч ампер. В этом случае короткое замыкание может вызвать перегрев проводов, пожар здания и т. д. Чтобы избежать этого, в такие цепи включают предохранители, в которых тонкий проводник АВ (рисунок 3) плавится при силе тока, превышающей ее допустимое значение для данной цепи, и размыкает цепь.
Последовательное соединение потребителей энергии тока
Последовательное соединение потребителей изображено на рисунке 4. Расчёт токов, напряжений и сопротивлений при таком соединении делают с помощью правил, приведенных ниже.
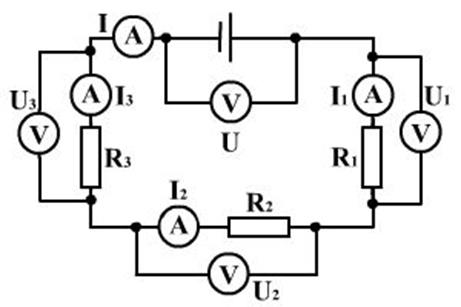
Рисунок 4 – последовательное соединение
Первое правило. При последовательном соединении сила тока во всех участках одинакова:
![]() .
(9)
.
(9)
Все амперметры на рисунке 4 показывают одинаковую силу тока. Объясняется это тем, что заряды в цепи не создаются и не уничтожаются. Индекс у обозначения силы тока при последовательном соединении ставить нет смысла.
Второе правило. При последовательном соединении напряжение на внешней цепи равно сумме напряжений на отдельных участках цепи:
![]() .
(10)
.
(10)
Это можно установить из опытов по показаниям вольтметров. (Объясните соотношение (10) на основании закона сохранения энергии.)
Третье правило. Напряжения на отдельных участках цепи при последовательном соединении прямо пропорциональны сопротивлениям участков:
![]() .
(11)
.
(11)
(Докажите это с помощью закона Ома и соотношения (9)).
Четвертое правило. При последовательном соединении эквивалентное сопротивление всей цепи равно сумме сопротивлений отдельных участков цепи:
![]() .
(12)
.
(12)
(Выведите это соотношение с помощью закона Ома и формулы (10).)
Из соотношения (10) видно, что при последовательном соединении п одинаковых участков цепи общее напряжение равно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.