Работа при перемещении электрического заряда. Движение заряженной частицы в однородном электрическом поле, вакууме; движение потока частиц; сила тока; плотность тока. Ток в металлах. Закон Ома для замкнутой цепи. Законы Кирхгофа. Виды соединения проводников, страница 21

Так как энергия в цепи не возникает и не исчезает, то сколько энергии заряд получает, столько же и теряет, пройдя всю замкнутую цепь. Поэтому

                                                                  .                                                    (21)

Если внешняя цепь состоит из неподвижных металлических проводников, эквивалентное сопротивление которых R, то U = IR, так как в этом случае вся электрическая энергия расходуется на тепловое действие. Заменяя в (21) напряжение Uчерез IR, получаем

                                                                  ,                                                   (22)

откуда

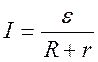                                                                   ,                                                   (22a)

Это соотношение называют законом Ома для всей цепи: сила тока в электрической цепи с одной э.д.с. прямо пропорцио­нальна электродвижущей силе и обратно пропорциональна сумме сопротивлений внешней и внутренней цепи.

Если пользоваться определенным источником электрической энергии, то ε и rв соотношении (21) можно считать постоянными величинами. Внешнюю цепь к этому источнику можно присоединять с разными сопротивлениями R. В зависимости от этого будут получаться различные значения тока I и напряжения U. Так как при этом сумма U+Irостается постоянной, то при увеличении I должно уменьшаться U', и наоборот.

Итак, чем больше сопротивление внешней цепи R, тем больше энергии единичный заряд расходует во внешней цепи и меньше во внутренней (Irуменьшается).

Когда Rвелико по сравнению с r, падение напряжения во внут­ренней цепи так мало по сравнению с U, что им можно пренебречь. Таким образом, при большом сопротивлении Rнапряжение на внеш­ней цепи Uприближенно равно э.д.с:

                                                                    .                                                         (23)

На этом основано измерение э.д.с. Действи­тельно, когда внешней цепи нет, то источник электрической энергии замкнут на вольтметр (рис 6б), который показы­вает падение напряжения IRна самом себе, равное U. А так как сопротивление вольтметра очень велико, то при этом справедливо соотношение (23).

Правила Кирхгофа

Реальные электрические цепи, т. е. соединенные между собой проводами источники тока (генераторы), потребители электро­энергии (нагрузки), сами провода включают в себя комбинации последовательно и параллельно соединенных нагрузок и генера­торов. В принципе рассчитывать разности потенциалов на всех участках цепи и силы токов в них, а также электродвижущие силы источников тока, входящих в данную цепь, можно с помо­щью закона Ома и закона сохранения заряда. Однако для упрощения расчетов Г. Кирхгофом были предложены два простых правила, нашедших широкое применение в электро- и радиотехнике.

Первое из них относится к узлам разветвления цепи, т. е. к точкам, в которых сходятся и из которых расходятся токи. Токи, подходящие к узлу, условились считать положительными, а токи, исходящие из узла - отрицательными. Таким образом, обходя замкнутую цепь в произвольном направлении, будем считать положительными те токи, направление которых совпа­дает с направлением обхода, и отрицательными те, направление которых противоположно направлению обхода. При этих усло­виях первое правило Кирхгофа формулируется так:

В каждой точке разветвления проводов (т. е. в узле) алгебраи­ческая сумма всех сил токов равна нулю:

                                                        .                                            (24)

Рассмотрим теперь замкнутую цепь, т.е. контур. Токи, теку­щие вдоль произвольно выбранного направления обхода контура, и э.д.с., полярность которой совпадает с этим обходом, будем считать положительными, а противоположные токи и э.д.с. - отрицательными. Иными словами, положительными э.д.с. будем считать те э.д.с, которые повышают потенциал в направлении обхода, т. е. э.д.с. будет положительной, если при обходе прихо­дится идти от минуса к плюсу внутри генератора. Тогда можно сформулировать второе правило Кирхгофа.