![]() ,
(29)
,
(29)
т. е. результирующее сопротивление равно сумме сопротивлений.
Доказательство этого положения студенты найдут самостоятельно, учитывая, что сила тока во всех резисторах одна и та же, а напряжение всей цепи равно сумме напряжений на отдельных резисторах.
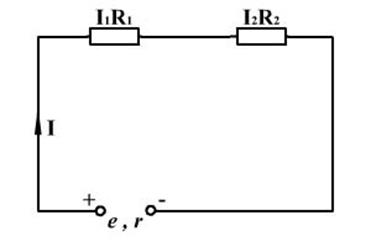
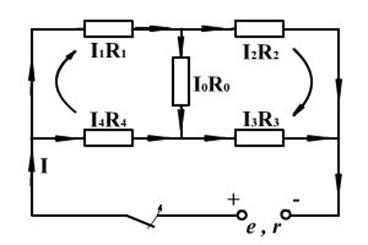
Рисунок 9 – электрическая цепь Рисунок 10 – мостовая схема
Измерение сопротивлений с помощью мостика Уитстона.Вэлектро- и радиотехнике применяют мостовую схему, в которой резисторы или другие элементы соединяют так, как изображено на рисунке 10. Можно подобрать такие значения сопротивлений R1, R2, R3иR4, что на участке с резистором R0, сила тока равна нулю (баланс моста). В этом случае I1 = I2 = I3. Обходя оба контура по часовой стрелке и учитывая, что I0 = 0, получим I1R1 - I4R4 = О и I2R2 - I3R3 = 0. Отсюда следует I1R1 - I4R4и I2R2 - I3R3. Разделив первое равенство на второе и сократив равные значения сил токов, найдем условие баланса моста:
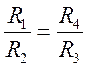 .
.
Это соотношение используют при вычислениях сопротивлений с помощью измерительной схемы - мостика Уитстона, предназначенного для сравнения сопротивлений. Здесь вместо резистора Rовключают чувствительный гальванометр, который фиксирует отсутствие тока в случае баланса. Тогда для определения искомого сопротивления, например R1, достаточно знать лишь сопротивление R2и отношение двух оставшихся сопротивлений.
На практике часто применяется реохордный мостик Уитстона. В нем последовательно соединенные резисторы R3и R4представляют собой одну калиброванную проволоку (реохорд). По проволоке скользит контакт, который делит проволоку длиной Lв определенном отношении l и L - l, равном отношению сопротивлений ее частей:
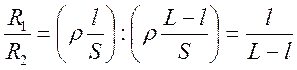 .
.
Отсюда 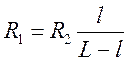 .
.
В качестве сопротивления R2используют эталонное сопротивление (магазин сопротивлений).
Проблемы тяговой сети постоянного тока
Любая электрическая цепь состоит из источника напряжения, устройства, потребляющего электрический ток, и соединительных проводов. На электрифицированных участках железных дорог источником напряжения являются так называемые тяговые подстанции, энергия от которых поступает к потребителю – электровозу по сети, которая тоже называется тяговой. В свою очередь, эта сеть состоит из четырех основных частей (рисунок 11) питающих проводов, контактной сети, рельсовой сети и отсасывающих проводов. Самая сложная часть такой электрической цепи – контактная сеть, поскольку ее конструкция должна надежно обеспечивать подачу энергии к движущимся локомотивам. Рельсовая сеть – это нити рельсов, электрически связанных друг с другом; питающие и отсасывающие провода (подземные кабели и воздушные линии) соединяют рельсовую сеть с тяговой подстанцией.
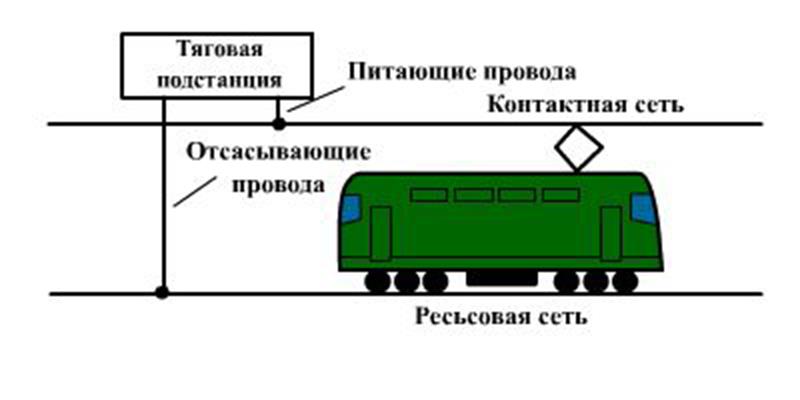
Рисунок 11 – Тяговая сеть постоянного тока
Электрификация железных дорог в нашей стране начиналась на постоянном токе при напряжении в контактной сети 3кВ (на магистральных линиях) и 1,5 кВ (на пригородных участках). В настоящее время на напряжение 3 кВ переведены практически все линии постоянного тока. Однако, напряжение, которое может быть подведено к применяемым на электровозах тяговым двигателям, заметно ниже: оно составляет от 750 В до 1600 В. Создание более высоковольтных двигателей затруднено тем, что при повышенных напряжениях резко возрастают трудности обеспечения надежной электрической изоляции отдельных элементов конструкции, которые (для снижения габаритов и веса всего двигателя в целом) приходится располагать близко друг к другу.
Известные нам из начального курса физики законы, описывающие протекание тока в электрической цепи, подсказывают выход, как использовать низковольтные двигатели при высоком напряжении в контактной сети: несколько двигателей на локомотиве можно соединить в одну группу последовательно, и тогда напряжение Ur , прикладываемое к такой группе, будет равно сумме напряжений, приложенных к каждому из ее элементов. Например, для группы из трех элементов (рисунок 12).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.