Работа при перемещении электрического заряда. Движение заряженной частицы в однородном электрическом поле, вакууме; движение потока частиц; сила тока; плотность тока. Ток в металлах. Закон Ома для замкнутой цепи. Законы Кирхгофа. Виды соединения проводников, страница 26

В третьем случае электрические и сторонние силы направлены в одну сторону. Поэтому заряды будут двигаться в ту же сторону. Это означает, что такой участок обязательно будет потребителем энергии, полученной из остальной цепи. Кроме того, под действием сторонних сил он получает дополнительную энергию. Итак, единичный заряд, получив энергию U от остальной цепи, на таком участке цепи получает ещё энергию ε и всю эту энергию U + ε расходует на тепловое действие, которое оценивается падением напряжения IR. Таким образом,

                                                                 IR=ε+U.                                              (7)

Определив I, получим закон Ома для такого участка цепи:

                                                                         I=(ε+U)/R.                                           (8)

Объединяя все три случая, можно следующим образом сформулировать закон Ома для участка цепи с э.д.с.: сила тока на участке цепи с э.д.с. прямо пропорциональна алгебраической сумме напряжения и э.д.с. на этом участке и обратно пропорциональна его сопротивлению.

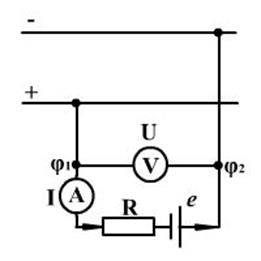
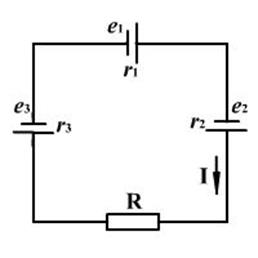
Рисунок 4 – Электрическая цепь                Рисунок 5 – Электрическая цепь

При расчетах, когда знак U или ε неизвестен, следует пользоваться формулой (7). Если в результате решения найденная величина U или ε окажется отрицательной, то это будет означать, что её действие на заряды в действительности обратно принятому при решении. Заметим, что для неразветвленной цепи с несколькими источниками э. д. с. закон Ома для всей цепи имеет вид:

                                             I=(ε_l+ε₂+... + ε_m)/(R₁+R₂+... + R_n)                                  (9)

Где m – число э.д.с. , а n – число сопротивлений во всей цепи. Здесь в числителе – алгебраическая сумма всех э.д.с. , причем э.д.с. на участке цепи положительна, если по направлению тока потенциал на этом участке возрастает; если же потенциал в этом направлении убывает, то значение э.д.с. берется с минусом. В знаменателе – сумма всех сопротивлений цепи.

Для схемы рисунка 4 формула (8) имеет вид

                                               I=(ε_l+ε₂+... ε_m)/(r₁+r₂+r₃ + R)                                     (10)

Работа электрического тока

Выясним, как вычисляется работа тока в электрической цепи. Полную работу тока на участке цепи, который является потребителем, можно найти по формуле

                                                     A_m=Uq                                                                 (11)

где U- напряжение на участке цепи, a q- заряд, перенесенный через поперечное сечение проводника за время прохождения тока t. Так как q = It, то

                                                     A_n=UIt                                                                  (12)

Поскольку напряжение и ток на участке цепи можно измерить вольтметром и амперметром, формула (11) удобна на практике для вычисления полной работы тока. По этой формуле работу можно вычислить независимо от того, в какой вид энергии на рассматриваемом участке цепи.

Когда вся электрическая энергия превращается во внутреннюю энергию (т.е. затрачивается на нагревание участка цепи), справедлива формула: I = U/R. Подставляя это выражение в (11), получим другую формулу для вычисления работы тока на участке цепи без э.д.с.:

                                                           A=U²t/R                                                     (13)

Поскольку U = IR, формулу (11) можно записать ещё следующим образом:

А = I²Rt

Итак, при вычислении работы тока на участке цепи без ЭДС можно пользоваться любой из формул.

Рассмотрим теперь участок цепи ЭДС. Вспомним, что когда у потребителя имеется противо – ЭДС, то электрическая энергия частично превращается во внутреннею энергию и частично в другие виды энергии. Электрическая энергия, израсходована в том случае, вычисляется по формуле (11). Остаётся установить, как подсчитать количество электрической энергии, которое превратилось во внутреннюю энергию на таком участке цепи.