6 В электрическом поле свободные электроны участвуют в направленном движении, которое иногда называют дрейфом. Хаотическое движение при этом сохраняется. Скорость дрейфа очень мала и составляет v ≈ 10-3м/с. Скорость направленного движения электронов зависит от напряжённости электрического поля v = k×E, где к -коэффициент пропорциональности, определяемый родом материала.
С помощью этой теории можно объяснить целый ряд явлений, в частности хорошую электропроводность металлов, термоэлектронную эмиссию, контактную разность потенциалов и др. В тоже время возможности теории довольно ограничены.
С помощью её нельзя объяснить такие явления, как проводимость металлов при сверхнизких температурах, проводимость полупроводников и т.д. Несмотря на эти недостатки, простота теории, хорошее соответствие выводов теории с опытными данными, делают её незаменимой, особенно в начале изучения электрических явлений в металлах.
Если в металлическом проводнике создать электрическое поле, то, как указывает теория, свободные электроны придут в направленное движение, т.е. будут дрейф навстречу электрическому полю.
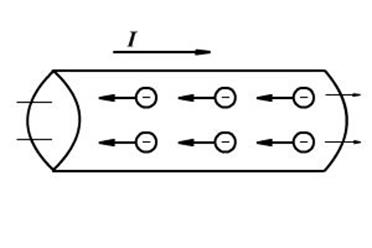
Ток в металлах представляет собой направленное движение свободных электронов.
Если электрическое поле внутри проводника не изменяется с течением времени, то такое поле называют стационарным.
В отличие от вакуума, в проводнике электроны будут взаимодействовать не только с электрическим полем, но и с кристаллической решеткой. Возникающая при этом сила будет препятствовать движению электронов, поэтому её называют силой сопротивления.
Наличие сопротивления приводит к тому, что свободные электроны под действием электрического поля будут медленно и равномерно двигаться внутри проводника.
v ≈ 10-3 м/с;
j = qonv;
I = qonvS
qo - заряд электрона, n - концентрация электронов в проводнике, v - скорость дрейфа.
Надо помнить, что кинетическая энергия направленного движения электронов очень мала, т.к. масса электронов и скорость их дрейфа весьма мала. Отсюда следует, что вся энергия, полученная свободными электронами от взаимодействия с электрическим полем, передается проводнику, по которому они движутся. В результате этого проводник может нагреваться, приходить в движение и т.д.
Закон Ома для участка цепи без ЭДС, сопротивление, удельное сопротивление, проводимость проводника, зависимость сопротивления металлов от температуры.
Допустим, что на участке цепи течет постоянный электрический ток I = const
Плотность тока j = qonkE
 |
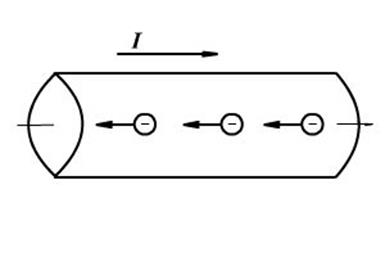
Произведение q0 nk зависит только от рода металла и называется удельной проводимостью j, а величину обратную удельной проводимости назвали удельным сопротивлением проводника.
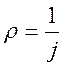 ;
;
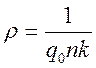 ;
;
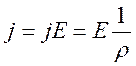 .
.
Наличие в проводнике стационарного поля позволяет утверждать, что Е = U/d = U/1
U - напряжение на концах проводника, а 1 - длина проводника.
J = U×l/pl;
I=j×S =U×S/pl
S/pl = G - проводимость проводника
Величину обратную проводимости называют сопротивлением проводника.
R = 1/G = pl/S;
R = pl/S;
I= U/R.
Сила тока на участке цепи прямопропорциональна напряжению и обратнопропорциональна сопротивлению участка.
Эту зависимость называют законом Ома для участка цепи.
U=1B;
I=1A;
R = B/A=1Oм.
Проводимость проводника при этом будет 1Си (Сименс) ρ = 1 Ом/м.
В довольно широком интервале температур, далёких от
абсолютного нуля, сопротивление металлического проводника является линейной
функцией температуры![]() , α - температурный коэффициент
сопротивления, единицей которого будет 1K-1.
, α - температурный коэффициент
сопротивления, единицей которого будет 1K-1.
При сверхнизких температурах многие металлы и сплавы перестают подчиняться этому закону, а их сопротивление скачком падает до нуля.
Это явление назвали сверхпроводимостью.
В 1987г. была открыта высокотемпературная сверхпроводимость.
Закон Ома для замкнутой цепи. Зависимость внешнего и внутреннего
напряжений от внешнего сопротивления цепи.
Применим закон Ома для замкнутой цепи с наличием в ней ЭДС.
I = U/R
В этом случае U = ∆φ + ![]() ; I =
(∆φ + ε)/R
; I =
(∆φ + ε)/R
Для замкнутой цепи ∆φ = О; I = ε/Rцепи
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.