Алгебраическая сумма произведений сил токов Iп в отдельных участках контура на их сопротивления Rn равна алгебраической сумме всех э.д.с., действующих в контуре, т. е.
. (25)
Например, для контура, схема которого дана на рис. 7 имеем
. (26)
Второе правило является следствием закона Ома для неоднородного участка цепи. В самом деле, пусть имеется контур, изображенный на рисунке 7. Здесь R2и R4- сопротивления источников ε1, и ε2, a I2и I4 - токи в них. Применяя к каждому из четырех участков сторон цепи контура закон Ома, запишем:
;
;
;
.
Суммируя левые и правые части равенств, получим (26) т. е. уравнение, соответствующее второму правилу (25). При расчетах цепей с помощью правил Кирхгофа не обязательно знать разности потенциалов на определенных участках. Правила Кирхгофа применяют следующим образом:
а) совершенно произвольно указывают стрелками направления токов на каждом из участков контура, а у источников тока отмечают знаки полюсов. Если после вычислений по правилам Кирхгофа сила тока на данном участке оказывается больше нуля, это означает, что истинное направление тока совпало с направлением, указанным стрелкой; в противном случае ток направлен противоположно.
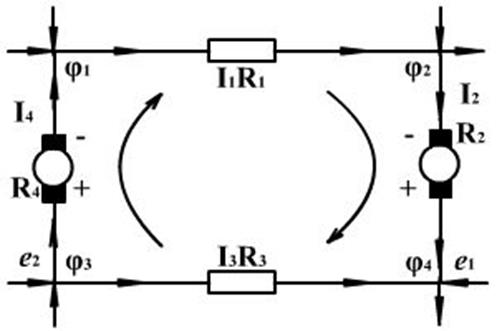
Рисунок 7 – правило Киргофа
б) в выбранном произвольном контуре все его участки обходят в одном направлении - либо по часовой стрелке, либо в противоположном. При этом слагаемое iRследует считать положительным, если направление обхода контура совпадает с на правлением тока. В противном случае это слагаемое отрицатель но. Далее, если направление обхода контура выбрано от положи тельного полюса источника к отрицательному, а внутри источника - от отрицательного к положительному, то э.д.с. источника считается положительной; в противном случае э.д.с. входит в уравнение со знаком минус;
в) произвольные контуры выделяют так, чтобы каждый новый контур содержал хотя бы один участок цепи, не вошедший в те уже рассмотренные контуры, для которых уравнения, со гласно второму правилу Кирхгофа, уже составлены.
Совокупность независимых уравнений, составленных по правилам Кирхгофа, оказывается достаточной, чтобы найти все токи, сопротивления или э.д.с. в разветвленной цепи. Задача сводится, таким образом, к решению системы линейных уравнений, в которой число уравнений должно совпадать с числом неизвестных величин.
Рассмотрим примеры применения правил Кирхгофа.
Расчет сопротивлений при параллельном соединении резисторов. Пусть два резистора с сопротивлениями R1и R2соединены параллельно (рисунок 8). Найдем их эквивалентное сопротивление и эквивалентную проводимость.
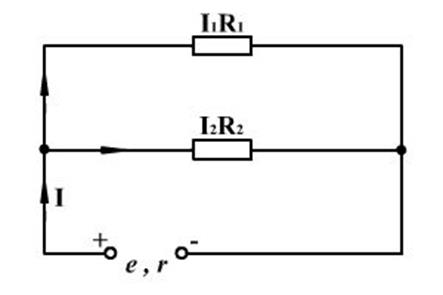
Рисунок 8 – два параллельных резистора
Применяя к узлу первое правило Кирхгофа, имеем
.
Для контура с единственным искомым эквивалентным сопротивлением R уравнение, согласно второму правилу, имеет вид
.
Для двух других контуров с сопротивлениями Rxи R2уравнения запишем так:
,
.
Решим систему четырех уравнений с четырьмя неизвестными. Вычитая из второго уравнения третье, получим IR – I1R1 = 0, откуда I1 = IR/R1. Аналогично, I2 = IR/R2. Подставив I1 и I2 в уравнение Кирхгофа для токов, после сокращений найдем эквивалентное сопротивление:
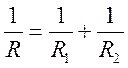, или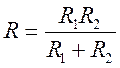 
. (27)
Учитывая, что проводимость g=1/R, получим
g= g1 + g2. (28)
Итак, при параллельном соединении резисторов эквивалентная проводимость цепи равна сумме проводимостей ее участков.
Отсюда следует, что при параллельном соединении резисторов их общее сопротивление меньше минимального. Заметим также, что в этом случае силы токов в разветвлениях обратно пропорциональны их сопротивлениям:
.
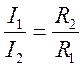Если резисторы с сопротивлениями R1и R2соединены последовательно (рисунок 9), то их эквивалентное сопротивление равно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.