Рівняння математичної фізики: Навчальний посібник

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ДОНБАСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

О. В. Мурга

РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ

Навчальний посібник

Рекомендовано Міністерством освіти і науки України

Алчевськ

2009

УДК  53:51

ББК  В 311

          М 91

Мурга Олена Владиславівна – ст. викл. кафедри радіофізики  Донбаського державного технічного університету ( м. Алчевськ).

Рецензенти:

І. В. Жихарєв – канд. фіз.- мат. наук, зав. кафедри фізики Луганського національного педагогічного університету ім. Тараса Шевченка (м. Луганськ);

В. І. Різун – канд. фіз.-мат. наук, проф. кафедри математичного аналізу Східноукраїнського національного університету ім. В. Даля (м. Луганськ).

Рекомендовано Міністерством освіти і науки України

як навчальний посібник для студентів вищих навчальних закладів

(Лист № 14/18.2-1145 від 01.06.2004)

М 91      Мурга О. В.

Рівняння математичної фізики: Навч. посіб. / О. В. Мурга –  Алчевськ: ДонДТУ, 2009 – 154 с.

ISBN 978-966-310-222-1

Навчальний посібник містить короткі відомості про теорію диференціальних рівнянь з частинними похідними, методику приведення таких рівнянь до канонічного вигляду. Дані уявлення про постановку задач для рівнянь в частинних похідних, що описує фізичні процеси, висловлені методи рішення цих задач. Включені задачі для самостійної роботи.

Призначені для студентів спеціальності радіофізика і електроніка.

УДК 53:51

ББК В 311

© О. В. Мурга, 2009

© ДонДТУ, 2009

© дизайн обкладинки

ISBN 978-966-310-222-1                                     О. М. Дика, 2009

ВСТУП

Рівняння математичної фізики виникли з розгляду найважливіших завдань, таких, як розповсюдження звуку в газах, хвиль в рідинах, тепло у фізичних тілах. У наш час активно вивчаються такі явища, як перенесення нейтронів в атомних реакторах, гравітація і електромагнітні ефекти, походження і розвиток Всесвіту. Всі ці розділи фізики створюють математичні моделі, які приводять до рівнянь з частинними похідними. Отже, рівняння математичної фізики – це розділ математики, який безпосередньо пов'язаний з вивченням складних явищ природи. Методи математичної фізики складають частину більш загальної теорії рівнянь з частинними похідними. Багато завдань теорії і практики приводять  до таких рівнянь. Число рівнянь обмежене, але кожне з них описує широкий круг явищ природи. Ця універсальність методів математичної фізики підкреслюється багатьма ученими.

Даний  посібник містить великий матеріал для проведення практичних занять і повністю відповідає програмі курсу «Методи математичної фізики», що читається в ДонДТУ для спеціальності «Радіофізика і електроніка». Його основна мета – допомогти студентам набути необхідних практичних навичок застосування теоретичних знань, отриманих на лекціях. Для цього в кожному розділі приведені приклади рішення задач, що ілюструють теоретичний матеріал, потім завдання і вправи з відповідями для самостійного розв’язання. Велика увага приділена методу розділення змінних.

Посібник написано на основі десятирічного досвіду викладання даного курсу для студентів-радіофізиків. Воно може бути корисним всім студентам технічних спеціальностей, а також всім особам, що цікавляться математичною фізикою і прикладною математикою.

1. ОСНОВНІ ПОНЯТТЯ

Диференціальні рівняння математичної фізики – це рівняння з частинними похідними, що зустрічаються при розв’язанні фізичних задач механіки, електрики, магнетизму, тощо. Будь-яку задачу математичної фізики можна розглядати як задачу розв’язання деякого диференціального рівняння з частинними похідними при певних додаткових умовах.  Важливе значення при розгляданні фізичних процесів  займає коректна постановка задач.

Поставити  задачу  означає:

1) вибрати вдало функцію (величину), яка характеризувала б даний фізичний процес (при цьому реальний фізичний процес замінюють деяким ідеальним процесом, але так, щоб зберігались основні властивості реального процесу), вибрати систему координат в залежності від умов задачі, але так, щоб шукана функція залежала від мінімальної кількості змінних;

2) використовуючи фізичні закони і співвідношення, скласти диференціальне рівняння для функції, що характеризує даний процес;

3) вставити початкові умови для шуканої функції, тобто записати значення фізичних характеристик, що описують даний процес в  початковий момент;

4) сформулювати крайові умови, тобто записати умови процесу на межі тіла, якщо розглядаємо нескінченний об’єм, то записуємо умови поведінки процесу на нескінченості.

Для ілюстрації основних методів математичної фізики розглянемо диференціальні рівняння з частинними похідними другого порядку і однією невідомою функцією.

Рівнянням в приватних похідних називають співвідношення

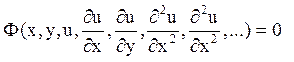                            (1.1)

що зв’язує незалежні змінні х, у, іскому функцію u = u(x,y) і її частинні похідні. Порядок, що відповідає старшій похідній рівняння називають порядком рівняння.

Функція u(x,y) безперервна в області D разом з своїми похідними, що входять врівняння, обертаюча це рівняння в тотожність, називається йогорішенням.

Рівняння другого порядку в частинних похідних має вигляд

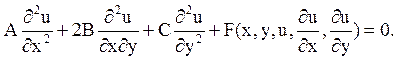          (1.2)

Це рівняння називають лінійним щодо старших похідних, якщо коефіцієнти  А, B, С  залежать тільки від x, у;  квазілінійним,якщо А, B, С  залежать від 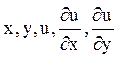; і лінійним, якщо  А, B, С  залежать тільки від х, у, а функціяF лінійна відносно.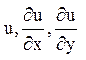

Загальний вид лінійного рівняння 2-го порядку:

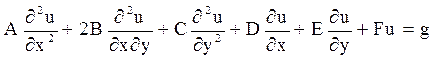            (1.3)

де    А,B,С, D, E, F, g – функції  х і у .

Якщо  g(x,y)¹ 0, то рівняння називається лінійним неоднорідним і лінійним однорідним, якщо  g(x,y) º 0.

Від коефіцієнтів рівняння (1.2) суттєво залежать характер і поведінка його рішень.

Рівняння виду (1.2)  в області D належить:

1)  гіперболічному типу, якщо в цій області  B²-AC>0;

2)     параболічному типу, якщо  B²- AC=0;

3)     еліптичному типу, якщо B²- AC<0.

 Рівняння

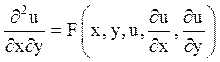
називається канонічним рівнянням гіперболічного типу;

рівняння

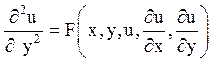
- канонічним рівнянням параболічного типу; 

рівняння

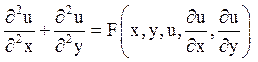
- канонічним рівнянням еліптичного типу.

Для  приведення рівняння (1.2) до канонічного вигляду, потрібно скласти рівняння характеристик

                     ,                         (1.4)

яке розпадається на два рівняння

,                           (1.5)

                         ,                         (1.6)

і знайти їх загальні інтеграли.

1. Покладемо B²-AC>0. Загальні інтеграли,  рівнянь (1.5) і (1.6) будуть речовинними і різними, вони визначають два різні сімейства речовинних характеристик. Відповідно до характеристик вводяться нові незалежні змінні . Похідні по старих змінних виражаються через похідні по нових змінних формулами:

,

,

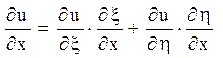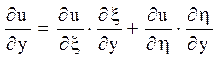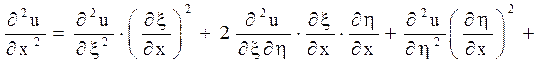
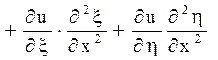,                               (1.7)

,

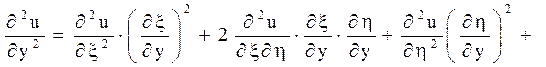
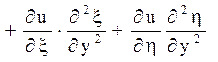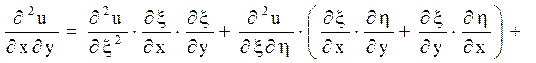
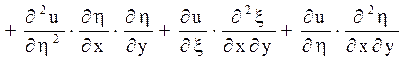
Підставляючи в рівняння (1.2) знайдені похідні, можна отримати канонічний вид рівняння гіперболічного типу

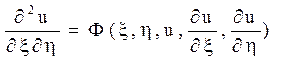
або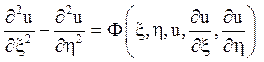                                   

Приклад 1. Привести до канонічного вигляду диференціальне рівняння:

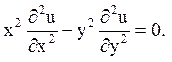
В даному разі  .