Физика \ Методы математической физики

Рівняння математичної фізики: Навчальний посібник, страница 3

При t=0:

Диференціювання функції (2.3) по t приводить до виразу:

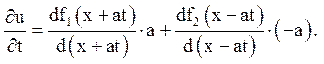
При t=0:

звідси

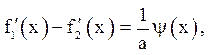
або                                     

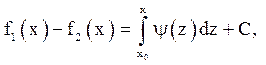
де  x0 и С – постійні.

З системи рівнянь

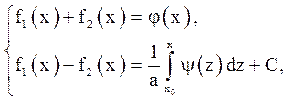
одержуємо

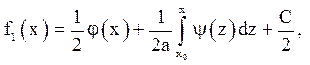
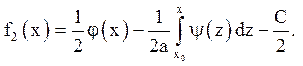
Підставляючи знайдені функції у вираз (2.З):

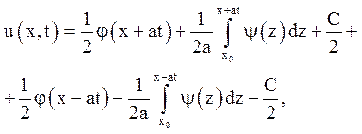
або 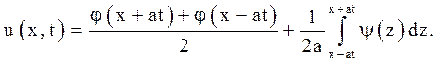               (2.4)

Отримана формула (2.4) носить назву формули Даламбера.

Приклад 1. Знайти рішення рівняння

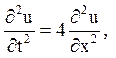
що задовольняє початковим умовам:

 

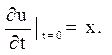
Для вирішення можна скористатися формулою Даламбера. В цьому випадку    а = 2,        тоді по формулі (2.4):

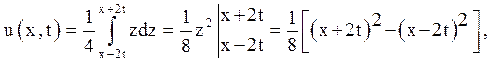
або                                                  

Легко перевірити, що отримана функція  задовольняє рівнянню і початковим умовам.

Приклад 2.  Знайти рішення рівняння

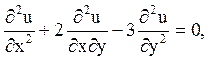
що задовольняє початковим умовам 

 

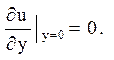
Складемо рівняння характеристик:

або 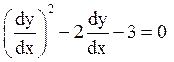, воно розпадається на два рівняння:  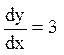і 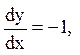 загальні інтеграли яких мають вигляд:  ; введемо нові змінні     і перерахуємо похідні

  

   

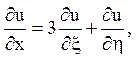
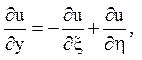
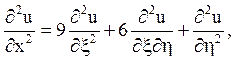
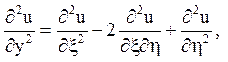
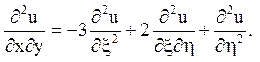
Канонічне рівняння має вигляд 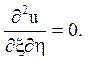 Загальне його рішення може бути представлено у вигляді суми двох довільних функцій . Значить, загальне рішення початкового рівняння має вигляд:

.

Для визначення функцій j і y слід задовольнити початковим умовам.

При           

Диференціювання функції   по у:

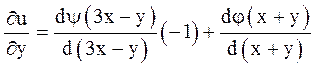
при    дає

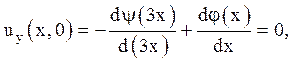
або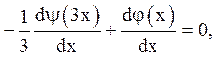                                  

що після інтегрування приводить до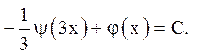  

З системи рівнянь

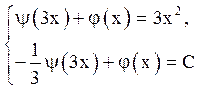
необхідно знайти функції j і y :

, 

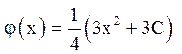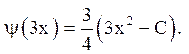
Покладемо  тоді 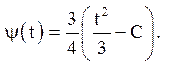 Підставимо знайдені функції j і y  в загальне рішення:

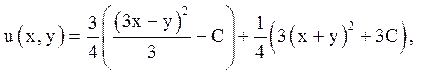
тобто  Легко переконатися, що ця функція дійсно задовольняє і рівнянню, і початковим умовам.

Задачі для самостійного розв’язування

1. Зайти загальний розв’язок рівняння:

1. uxx + 4uxy  + 3uyy = 0,

3. uxx + 6uxy + 5uyy = 0,

5. uxx + 4uxy - 21uyy = 0,

7. uxx – 2uxy - 24uyy = 0,

9.  uxx - 8uxy + 16uyy - ux + 4uy = 0,

11. uxx + 2uxy+ uyy+ 5ux - 5uy = 0,

13.  uxx - 2uxy + uyy - 3ux + 3uy = 0,

15. uxx – 4uxy+ 4uyy+ 2ux - 4uy = 0,

17.  uxx + 4uxy + 4uyy +ux – 2uy = 0,

19. uxx + 4uxy + 5uyy  = 0,

21. uxx + 6uxy + 13uyy  = 0,

 23. uxx + 4uxy + 20uyy  = 0,   

Відповідь:

1. u = C1(y - 3x) + C2(y - x),

3. u = C1(y - 5x) + C2(y - x),

5. u = C1(y - 7x) + C2(y + 3x),

7. u = C1(y - 4x) + C2(y + 6x),

 9. u = C1(y + 4x) + C2(y + 4x) e-y/4,

11.u = C1(y – x) + C2(y – 2x) e-5y,

13. u = C1(y + x) + C2(y + x) e3y,

15. u = C1(y + 2x) + C2(y + 2x) e-y,

17.u = C1(y – 2x) + C2(y – 2x) e-y/2,

19. u = Ref(y – 2x + xi),

21. u = Ref(y – 3x + 2xi),

23. u = Ref(y – 2x + 4xi),

2. uxx - 2uxy - 3uyy = 0,

4. uxx - 4uxy - 12uyy = 0,

6. uxx - 6uxy + 8uyy = 0,

8. uxx - 4uxy -  32uyy = 0,

10. uxx – 4uxy+ 4uyy+ ux + 2uy = 0,

12.  uxx + 6uxy + 9uyy + 2ux – 6uy = 0,

14. uxx – 6uxy + 9uyy + 2uх – 6uy  = 0,

16.  uxx + 22uxy + uyy - ux + 2uy = 0,

18. uxx + 8uxy+ 16uyy+ 3ux - 12uy = 0,

20.  uxx – 4uxy  + 8uyy = 0,

22. uxx – 6uxy  + 18uyy = 0,

24. uxx –  4uxy  + 40uyy = 0.

2. u = C1(y - x) + C2(y + 3x),

4. u = C1(y - 2x) + C2(y + 6x),

6. u = C1(y + 2x) + C2(y + 4x),

8. u = C1(y - 4x) + C2(y + 8x).

10. u = C1(y – 2x) + C2(y – 2x) e-y2,

12. u = C1(y – 3x) + C2(y – 3x) e-2y/3,

14. u = C1(y +3x) + C2(y – 3x) e2y/3,

16. u = C1(y – x) + C2(y – x) ey,

18. u = C1(y – 4x) + C2(y – 4x) e-3y/4,

20. u = Ref(y + 2x + 2xi),

 22. u = Ref(y + 3x + 3xi),

 24.  u = Ref(y + 2x + 6xi).

2. Користуючись формулою Даламбера, розв’язати задачі:

а)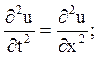            

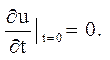
Відповідь:        

б)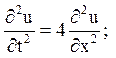                     

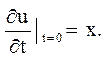
Відповідь:             

в)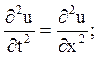            

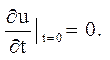
Відповідь:         u(x,t) = sinx×cosat.

г)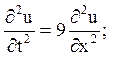            

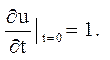
Відповідь:         u(x,t) = 1+t.

3. Знайти загальне рішення наступних рівнянь:

а)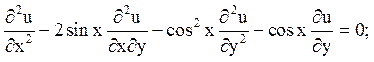   

б)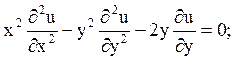   

в)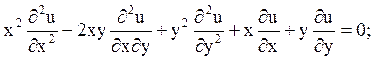   

г)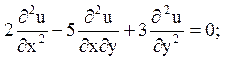    

д)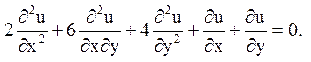   

Відповідь:   а)

б)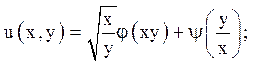  

в)   

г)    

д)   

4. Знайти рішення рівняння:

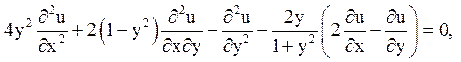
що задовольняє початковим умовам:

 

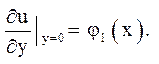
Відповідь: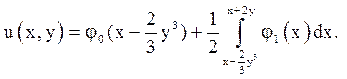   

5. Знайти рішення рівняння:

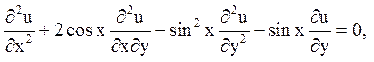
що задовольняє початковим умовам:

 

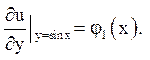
Відповідь:.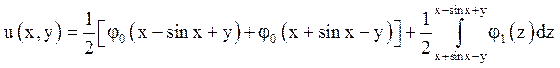

6. Знайти рішення рівняння:

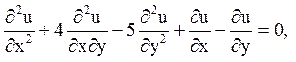
що задовольняє початковим умовам:

 

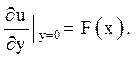
Відповідь: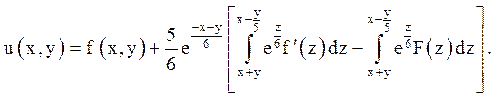  

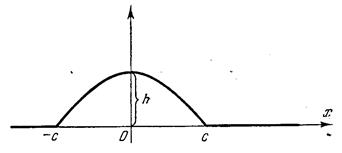
7. Необмежена струна збуджена локальним початко-вим відхиленням, що має форму квадратичної параболи. Знайти: а) формули, що представляють профіль струни при t > 0, і

б) формули, що представляють закон руху точок струни з різними абсцисами при t > 0.

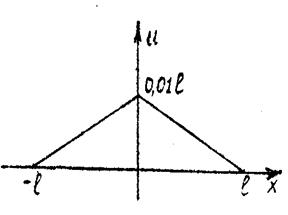
8. Знайти закон коливання нескінченної струни, якщо початкове відхилення задається рівністю:

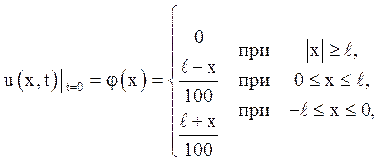
де  – заданий відрізок. Початкова швидкість і зовнішня   сила що вимушує дорівнює нулю. Побудувати на кресленні профіль струни в різні моменти часу. Графік функції приведений на рисунку.

3. МЕТОД відокремлення ЗМІННИХ ДЛЯ ЗАДАЧІ ПРО ВІЛЬНІ КОЛИВАННЯ СТРУНИ, закріпленої НА КІНЦЯХ

Задача про вільні коливання струни, закріпленої на кінцях, зводиться до рішення однорідного рівняння

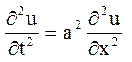                                          (3.1)

за початкових умов

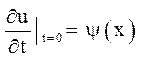                     (3.2)

і крайових умовах

                                   (3.3)

Метод відокремлення змінних (метод Фур’є) полягає в тому, що спочатку розшукуються нетривіальні рішення рівняння (3.1), що задовольняють крайовим умовам (3.3),  у вигляді добутку двох функцій, одна з яких залежить тільки від х, а інша тільки від t

                                    (3.4)

а потім задовольняються початкові умови (3.2).

Диференціюючи двічі  функцію (3.4)  по x і по t, отримаємо

                   

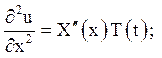
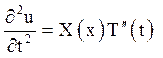
і підставимо ці похідні в рівняння (3.1):

Розділимо змінні

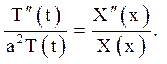                                    (3.5)

Щоб функція (3.4) була рішенням рівняння (3.1), рівність (3.5) повинна дотримуватися при всіх значеннях x і t. Значить, обидві частини рівності (3.5) не повинні залежати ні від x, ні від t, тобто

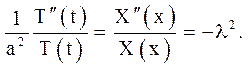                        (3.6)

Важливо помітити, що якщо в співвідношеннях (3.6) узяти ненегативну постійну, то виходять тільки тривіальні рішення.

Звідси витікає, що функції T(t) і Х(x) повинні задовольняти звичайним диференціальним рівнянням:

     и     

Скачать файл