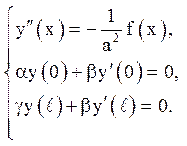 (6.2)
(6.2)
Тоді для відшукання функції W(x,t) вимагається вирішити задачу
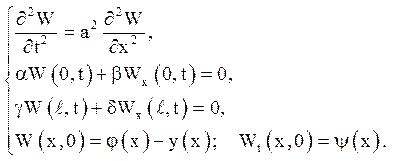 (6.3)
(6.3)
Остання задача вже достатньо знайома і розв'язується методом Фур’є. Залишилося вирішити задачу (6.2). Після інтегрування рівняння вийде
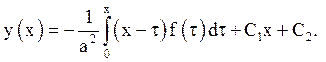
Постійні С1 і С2 знаходяться з крайових умов.
Приклад 1. Вирішити рівняння
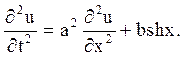
за нульових початкових і крайових умов ![]()
![]() Рішення
розшукується у вигляді суми
Рішення
розшукується у вигляді суми ![]() Потім слід цю
суму підставити в рівняння
Потім слід цю
суму підставити в рівняння
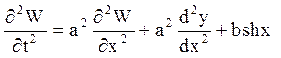
і підібрати функцію ![]() так, щоб
так, щоб 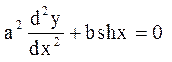 і
і ![]() Рівняння
Рівняння
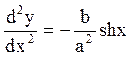 інтегрується двічі:
інтегрується двічі:
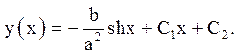
З крайових умов ![]()
![]() визначаються
визначаються ![]()
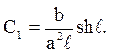
Значит,
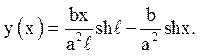
Функція W(x,t)- є рішення наступної задачі:
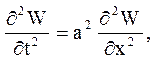
![]()
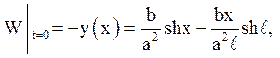
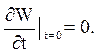
Подібні задачі розглядалися в розд. 3, тому можна відразу записати рішення:
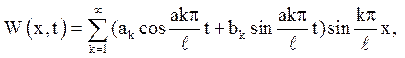
де
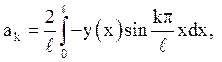
![]()
Залишається обчислити
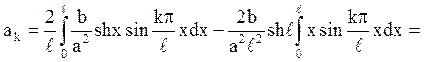
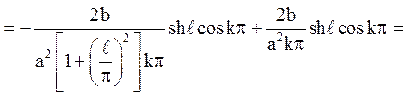
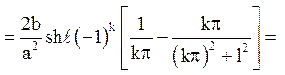
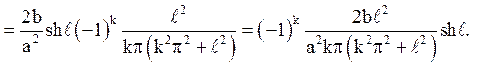
Відповідь:
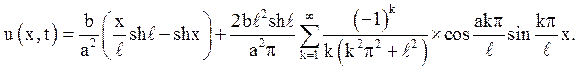
1. Застосуйте правило 4 до рішення задачі 5 розд. 4.
2.Сформулюйте правило 4 для випадку гармонійних зовнішніх сил (задачі 1, 2 і 4 розд. 4).
Метод Фур’є з успіхом застосовується при дослідженні коливань прямокутної мембрани.
Приклад. Однорідна квадратна мембрана, що має в початковий момент часу t
= 0 форму ![]() ,
де А – постійна, почала коливатися без початкової швидкості. Дослідити вільні
коливання мембрани, закріпленої по контуру х = 0,
х = l, у = 0, у = l.
,
де А – постійна, почала коливатися без початкової швидкості. Дослідити вільні
коливання мембрани, закріпленої по контуру х = 0,
х = l, у = 0, у = l.
Рівняння вільних коливань мембрани має вигляд
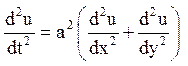 (7.1)
(7.1)
Тут u = u (x, у, t) – відхилення точок мембрани від площини ХОY у момент t. Умова закріплення мембрани по краях запишеться таким чином:
u|x=0 = u|x=l = u| y=0 = u |y=l (7.2)
Початкові умови
U|t=0 = Aху(l – x) (l – у); 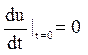 (7.3)
(7.3)
Шукаємо рішення даної задачі у вигляді
u(x, у, t)= T(t) X(x) У(у).
Підставимо функцію u(x, у, t ) в рівняння і розділимо змінні
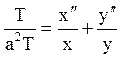
Хай
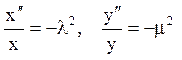 .
.
Для задачі
х"+l2х = 0, х(0)= 0, х(l) = 0,
отримаємо власні значення
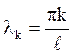 , (7.4)
, (7.4)
власні функції
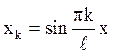 , k=1,2,... (7.5)
, k=1,2,... (7.5)
Для задачі
y" + m2y = 0, y(0) = 0, y(l) = 0
отримаємо 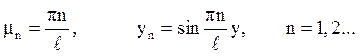
Переходимо до відшукання функції Т(t): рівняння
Т + а2(l 2+m2)Т=0
маємо рішення
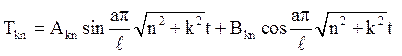
З умови 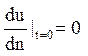 виходить, що Т'(0)=0. Обчислюємо
виходить, що Т'(0)=0. Обчислюємо
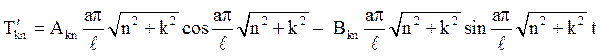
![]()
Підставляючи t = 0, отримаємо Аkn=0. Отже
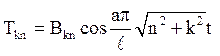 .
.
Тоді
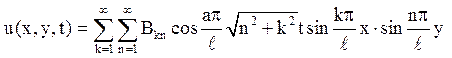
Застосовуючи умову u|t=0 = Axy(l–x)∙(l–y), отримаємо
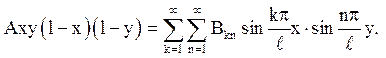
Справа отримали подвійний ряд Фур’е. Значить, коефіцієнти ряду Фур’е для заданого початкового відхилення дорівнюють
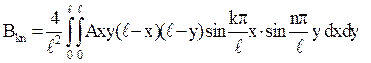 .
.
Переходячи від подвійного інтеграла до повторного, отримаємо
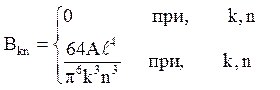
Відповідь:
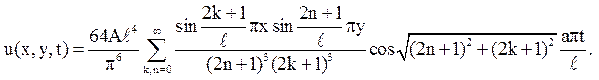
1. Знайти закон
вільних коливань квадратної мембрани із стороною
l, якщо в початковий момент мембрані додана
швидкість 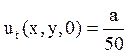 (де а - постійна, що фігурує в рівнянні мембрани).
Початкове відхилення дорівнює нулю. Мембрана закріплена в точках свого контуру.
(де а - постійна, що фігурує в рівнянні мембрани).
Початкове відхилення дорівнює нулю. Мембрана закріплена в точках свого контуру.
Відповідь:
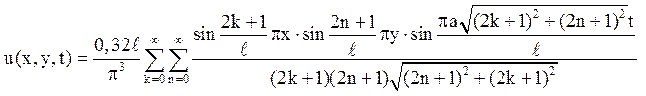
2. Знайти закон вільних коливань квадратної мембрани із стороною l, якщо в початковий момент відхилення в кожній точці визначалося рівністю
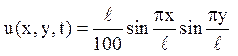
Початкова швидкість дорівнює нулю. Уздовж контуру мембрана закріплена.
Відповідь: 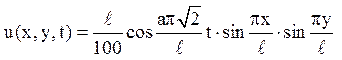 .
.
1. Початкові і граничні умови. Розподіл температури в стрижні описується наступним рівнянням (рівняння теплопровідності)
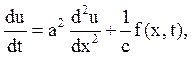 (8.1)
(8.1)
де f(x,t) – потужність внутрішніх джерел в стрижні, розрахована на одиницю маси, c – коефіцієнт питомої теплоємності.
В початковий момент часу t = 0 розподіл температури вважається відомим
u(x,0)= j(x) (8.2)
При стрижні кінцевих розмірів задаються умови на його кінцях (граничні умови). Можливі наступні типи граничних умов:
a) на кінцях підтримується задана температура (заданий тепловий режим):
u(0,t)= g1(t), u(l,t) = g2(t)
б) на кінцях стрижня задана величина теплового потоку q
q|x=0 = f1(t), q|x=l = f2(t).
(Усюди нижче величина q позначає потік, направлений з тіла в зовнішнє середовище). Оскільки
потік пропорційний ![]() і на кінцях направлений в
різні боки, то
і на кінцях направлений в
різні боки, то
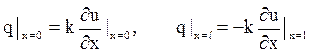 (8.3)
(8.3)
Тому граничні умови мають вигляд
ux(0,t)= q1(t), ux(l,t) = q2(t)
де q1(t)=k-1f1(t), q2(t)=k-1f2(t)
в) на кінцях відбувається теплообмін з середовищем. Хай q(t) – температура зовнішнього середовища. Припускаємо, що теплообмін відбувається за законом Ньютона.
Закон Ньютона. Величина теплового потоку через межу тіла пропорційна різниці температур тіла і зовнішнього середовища:
q| через межу = l [u (s,t) - q (t)]
де u(s,t) – температура тіла на межі, а q (t) – температура середовища.
Зокрема, для стрижня
q|x=0= l [u (0,t) - q (t)], q|x=l = l [u (l,t) - q (t)]
або згідно (8.3)
ux(0,t) – hu(0,t)=q1(t)
ux(l,t) - hu (l,t) = q2(t)
де 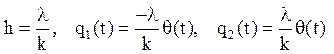 .
.
г) кінці стрижня теплоізольовані. Це означає, що на кінцях відсутній тепловий потік. Тому крайові умови матимуть вигляд
ux(0,t)=0, ux(l,t)=0.
2. Метод Фур’є для однорідної задачі. Розглянемо розповсюдження тепла в стрижні кінцевої довжини, коли на його кінцях підтримується нульова температура. Джерела тепла в стрижні відсутні, початкова температура в кожній точці стрижня задана. Температура u(x,t) стрижня є рішення задачі.
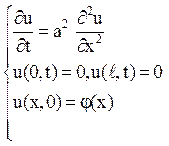
![]() (8.4)
(8.4)
Шукаємо спочатку нетривіальні рішення рівняння, що задовольняють крайовим умовам, у вигляді
U(x,t)=X(x)T(t).
Слідуючи знайомій схемі, отримаємо
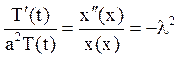
Власні значення 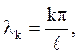 власні функції
власні функції 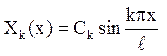 .
.
Кожному власному значенню lк відповідає функція Тk(t), що задовольняє рівнянню першого порядку:
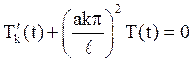
Загальне рішення цього рівняння має вигляд
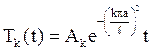
Значить, приватні рішення однорідного рівняння теплопровідності, що задовольняють однорідним граничним умовам, представляються у вигляді:
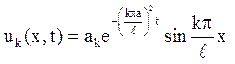
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.