Рівняння математичної фізики: Навчальний посібник, страница 12

Х"(х) - l²Х(х)= 0                                                (8)

і крайовим умовам.

Х(0)= 0,     Х (с) = 3                                            (9)

Загальне рішення рівняння (8) має вигляд

Х(х)= С₁е^lх + С₂е ^–lх

крайові умови дають

Х(0)= С₁ + С₂ = 0    = >    С₁ = - С₂

Х(с)= С₁ е^lх + С₂е ^–lх = 3.

Значить

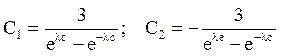
і рішення задачі (8) – (9) має вигляд

 

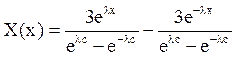
або

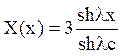                                                     (10)

Залишилося підставити знайдену функцію X(x) (10) і функцію V(у,z)(5) в рівняння  (3):

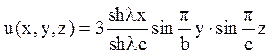                                  (11)

тут

.

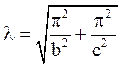Легко перевірити, що функція (11) дійсно задовольняє і рівнянню (1) і крайовим умовам (2).

Задачі для самостійного розв’язування

1. Знайти рішення рівняння Лапласа в напівсмузі 0 £ х £ а; 0£ g £ ¥, задовольняюче крайовим умовам  u(0,y)=0; u(а, у)=0; 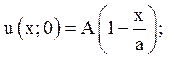 u(x,µ)=0.

Відповідь:                      

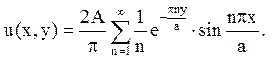
2. Знайти, рішення рівняння Лапласа в прямокутнику D: 0 £ x£ а; 0 £ у£ b, задовольняюче крайовим умовам

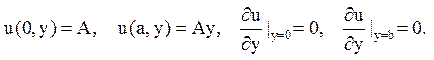
Відповідь:

 

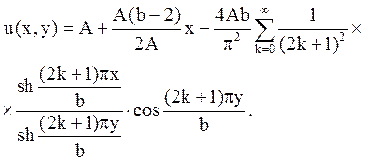
3. Написати рішення другої крайової задачі для рівняння  Du = 0 усередині круга, якщо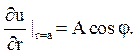

Відповідь: u(r,j) = A₀+Arcosj, де А₀ – довільна  постійна.

4. Написати рішення другої крайової задачі для рівняння   Du = 0 зовні круга, якщо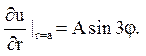 

Відповідь:                  .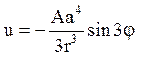

5. Знайти рішення: а) внутрішньої і б) зовнішньої крайових задач для рівняння Лапласа, якщо на межі круга задані умови:

1)  u|_p=a = Asinj;

2) u|_p=a=Asin³j + B;

3) u|_r=a=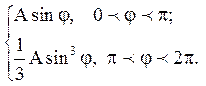

Відповідь:

а) рішення внутрішніх задач мають вигляд:

 1)

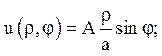
2)

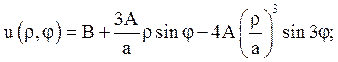
3)  

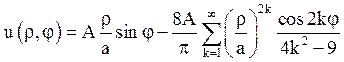
б) рішення зовнішніх крайових задач даються виразами:

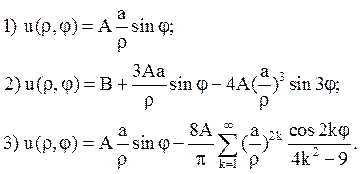
6. На межі тонкої пластинки у формі кругового сектора  r£ а; 0 £ j £ a задана температура

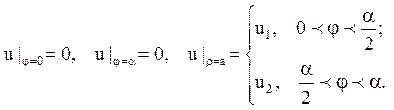
Знайти стаціонарне термічне поле в пластинці.

Відповідь:                  

 

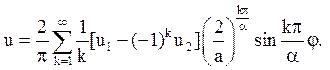
7. Вирішити рівняння Лапласа усередині кільцевого сектора, обмеженого дугами кіл r = а, r = b і кутами  j = 0,   j = a, якщо задані наступні умови на межах

u = 0  при  j = 0,  j = a,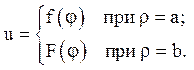     

Відповідь:

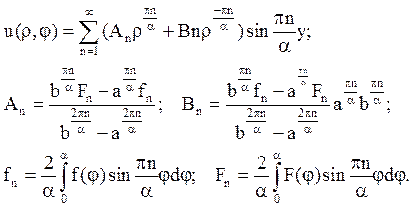
8. Знайти рішення рівняння  в колі < r <, якщо(А, ,- надані числа).

Відповідь:  .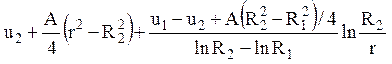

9. Знайти рішення рівняння Лапласа   у прямокутнику  0<х<a, 0<y<b, якщо на межі цього багатокутника  приймає наступні значення:

          

                 

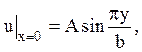
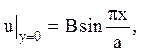
Відповідь:  .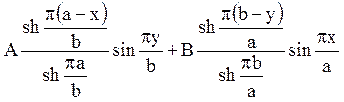

Вказівка. Рішення шукати у вигляді де  і  - гармонійні функції такі, що ,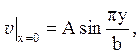  

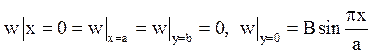
10. Знайти стаціонарне розподілення температури в прямокутній одноріднії пластини 0<х<a, 0<y<b, якщо її сторони x=a і  y=b вкриті тепловою ізоляцією, дві інші (x=0, y=0) підтримуються при нульовій температурі, а в пластинці виділяється тепло  з постійною щільністю q.

Відповідь: 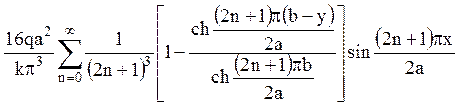, k – коефіцієнт внутрішньої теплопровідності.

Вказівка. Завдання зводиться до вирішення рівняння 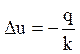 за умови , .

11. Дано тонку прямокутну пластинку зі сторонами , , які збігаються з осями координат. Для цієї пластини відомим є початковій розподіл температури. Бічні сторони , під час спостереження підтримуються при нульовій температурі, а обидві основи мають заданий розподіл температури:

, , .

Знайти температуру будь – якої точки в момент часу .

Відповідь :

.

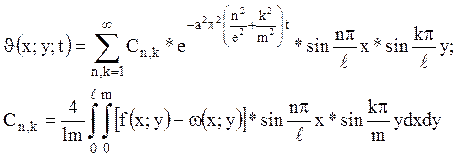12. Знайти розподіл потенціалу електростатичного поля  всередині прямокутника ОАСВ, у якого вздовж сторони ОВ потенціал дорівнює , а три інші сторони заземлені. Електричні заряди всередині прямокутника відсутні.

Відповідь:

 

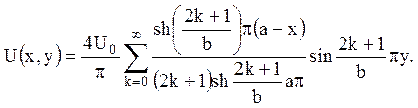
Література

1. Тихонов А.Н. Уравнения математической физики. / А.Н. Ти-хонов, А.А. Самарский. – М.: Наука,  1972. – 736 с.

2. Соболев С.Л.  Уравнения математической физики. / С.Л. Со-болев – М.: Наука, 1966. – 444 с.

3. Владимиров В.С. Уравнении математической физики. / В.С. Владимиров. – М., 1967. – 436 с.

4. Мышкис А.Д. Математика для втузов. Специальные курсы. / А.Д. Мышкис. – М., 1971. – 632 с.

5. Сборник задач по уравнениям математической физики / под ред. В.С. Владимирова) – М.: Наука,  1982. – 256 с.

6. Самарский А.А. Сборник задач по уравнениям с частными производными. / А.А. Самарский.  – М.: Наука, 1972. – 736 с.

7. Смирнов М.М. Задачи по уравнениям математической физики. / М.М. Смирнов. – М.: Наука, 1965. – 98 с.

ЗМІСТ

1. ОСНОВНІ ПОНЯТТЯ.. 4

Задачі для самостійного розв’язування. 18

2. МЕТОД ХАРАКТЕРИСТИК. ФОРМУЛА ДАЛАМБЕРА.. 25

Задачі для самостійного розв’язування. 32

3. МЕТОД відокремлення ЗМІННИХ ДЛЯ ЗАДАЧІ ПРО ВІЛЬНІ КОЛИВАННЯ СТРУНИ, закріпленої НА КІНЦЯХ.. 38

Задачі для самостійного розв’язування. 48

4. РІШЕННЯ НЕОДНОРІДНИХ ЗАДАЧ ДЛЯ РІВНЯННЯ коливань. 55

Задачі для самостійного розв’язування. 71

5. метод фур’є  для струни  з  ЗАДАНИМИ СИЛАМИ НА КІНЦЯХ   76

Задачі для самостійного розв’язування. 86

6. БІЛЬШ ПРОСТЕ ПРАВИЛО У ВИПАДКУ СТАЦІОНАРНИХ ЗОВНІШНІХ СИЛ.. 89

Задачі для самостійного розв’язування. 93

7. ЗАСТОСУВАННЯ МЕТОДУ  ФУРЬЕ ДЛЯ ДВУМЕНРНОЙ ЗАДАЧІ ПРО КОЛИВАННЯ МЕМБРАНИ.. 94

Задачі для самостійного розв’язування. 97

8. МЕТОД ФУР’Є ДЛЯ ОДНОРІДНОГО РІВНЯННЯ ТЕПЛОПРОВІДНОСТІ 99

Задачі для самостійного розв’язування. 118

9.  Метод Фур’є для рівняння Лапласа.. 128

Задачі для самостійного розв’язування. 146

Навчальне видання

О.В. Мурга

РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ

Навчальний посібник

В авторській редакції

Комп’ютерна верстка                                     Н.Б. Трофімова

Дизайн обкладинки                                        О.М. Дика

_____________________________________________________________

Підп. до друку  08.05.2009. Формат 60х84 ¹/₁₆. Папір офс.

Друк RISO. Ум. друк. арк. 9,62. Зам. № 175. Наклад 35  пр.

Видавництво не несе відповідальності за зміст матеріалу, наданого автором до друку.

Видавець та виготівник:

Донбаський державний технічний університет

94204, Луганська обл., м. Алчевськ, пр. Леніна, 16.

(ТВО "Ладо", ауд. 2113, т/факс 2-02-59)

E-mail: info@dmmi.edu.ua   Web-site: http//www.dmmi.edu.ua

Свідоцтво Держкомтелерадіо серія ДК, № 2010 від 12.11.2004