![]()
![]()
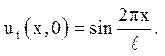
Відповідь: 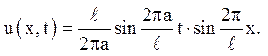
6. Знайти закон коливання
струни завдовжки l, розташованої на відрізку [0,![]() ], якщо в початковий момент їй надали
форму кривої
], якщо в початковий момент їй надали
форму кривої 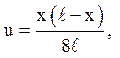 а потім відпустили без початкової швидкості. Струна
закріплена на кінцях. Зовнішні сили відсутні.
а потім відпустили без початкової швидкості. Струна
закріплена на кінцях. Зовнішні сили відсутні.
Відповідь:
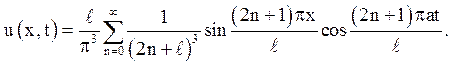
7. Знайти закон коливання струни завдовжки l,
якщо в початковий момент всі точки струни повідомлена швидкість, рівна ![]() (де а – постійна, фігуруюча в рівнянні
струни). Початкове відхилення відсутнє. Кінці струни закріплені. Зовнішні сили
відсутні
(де а – постійна, фігуруюча в рівнянні
струни). Початкове відхилення відсутнє. Кінці струни закріплені. Зовнішні сили
відсутні
Відповідь:
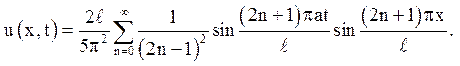
8. Однорідна струна завдовжки l,
закріплена на обох кінцях, знаходиться в прямолінійному положенні рівноваги. В
деякий момент часу, що приймається за початковий, вона одержує в точці х = с удар
від молоточка, який повідомляє цій точці постійну швидкість ![]() 0. Знайти відхилення
0. Знайти відхилення ![]() струні для будь-якого моменту часу.
струні для будь-якого моменту часу.
Розглянути два випадки.
а) Струна збуджується початковою швидкістю
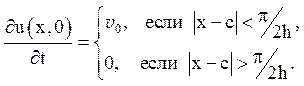
Цей випадок
відповідає плоскому жорсткому молоточку, що має ширину ![]() і ударяє в точці х = с.
і ударяє в точці х = с.
б) Струна збуджується початковою швидкістю
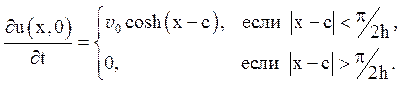
Цей випадок
відповідає жорсткому опуклому молоточку вширшки ![]() . Такий молоточок в центрі інтервалу порушує
найбільшу швидкість.
. Такий молоточок в центрі інтервалу порушує
найбільшу швидкість.
Відповідь:
а) 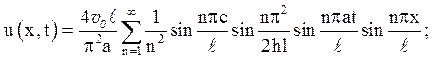
б) 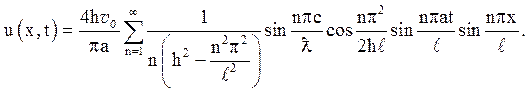
9. Вирішити першу змішану задачу для однорідного хвильового рівняння на відрізку
|
а). utt = xxx, x Î (0,2), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(2 – x), u(0,t) = u(2,t) = 0 б). utt = 2uxx, x Î (0,1), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(1 – x), u(0,t) = u(1,t) = 0 в). utt = 3uxx, x Î (0,3), t Î (0,¥), u(x,0) = 0, ut(x,0) = x(3 – x), u(0,t) = u(3,t) = 0, г). utt = 4uxx, x Î (0,2), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(2 – x), u(0,t) = u(2,t) = 0, д). utt = uxx, x Î (0,2), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(1 – x), u(0,t) = u(1,t) = 0, е). u(x,0) = 0, ut(x,0) = x(4 – x), u(0,t) = u(4,t) = 0, ж). u(x,0) = 0, ut(x,0) = x(3 – x), u(0,t) = u(3,t) = 0, з). utt =9 uxx, x Î (0,2), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(2 – x), u(0,t) = u(2,t) = 0, и). utt = 16uxx, x Î (0,2), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(2 – x), u(0,t) = u(2,t) = 0, к). utt = uxx, x Î (0,3), t Î (0,¥) u(x,0) = 0, ut(x,0) = x(3 – x), u(0,t) = u(3,t) = 0, Відповідь: а). б). в). г). д). е). ж). з). и). к). |
Метод відокремлення змінних дозволяє також знайти рішення неоднорідного рівняння коливань. Малі поперечні коливання пружної струни описуються рівнянням
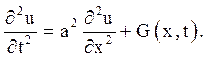 (4.1)
(4.1)
Функція ![]() визначає відхилення u точки
струни у момент часу t. Графік функції
визначає відхилення u точки
струни у момент часу t. Графік функції ![]() при кожному фіксованому значенні t представляє форму
струни, що коливається, у цей момент часу. Функція
при кожному фіксованому значенні t представляє форму
струни, що коливається, у цей момент часу. Функція ![]() густина зовнішніх сил, розрахованих на
одиницю маси струни,
густина зовнішніх сил, розрахованих на
одиницю маси струни, ![]() позитивна постійна (Т – натягнення струни r - густина
її). В початковий момент часу t=0
передбачаються відомими положення струни і її швидкість:
позитивна постійна (Т – натягнення струни r - густина
її). В початковий момент часу t=0
передбачаються відомими положення струни і її швидкість:
![]()
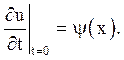 (4.2)
(4.2)
Якщо струна має кінцеві розміри ![]() , то потрібна додаткова
інформація про поведінку рішення
, то потрібна додаткова
інформація про поведінку рішення ![]() на кінцях
на кінцях ![]() ,
, ![]() .
.
Можливі наступні типи крайових умов:
а) струна закріплена на кінцях:
![]()
![]() (4.3)
(4.3)
б) струна не закріплена на кінцях і відомий закон руху кінців:
![]()
![]() (4.4)
(4.4)
У такому разі прийнято говорити, що заданий режим на кінцях;
в) кінці струни не закріплені і відомі сили G1(t), G2(t), діючі на кінцях. Тоді за законом Гука
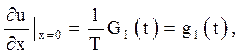 (4.5)
(4.5)
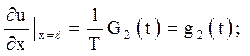
г) кінці струни закріплені пружно:
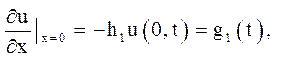 (4.6)
(4.6)
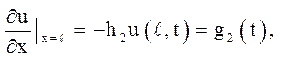
де h1, h2
– постоянные ![]()
![]()
д) кінці струни вільні (під цим розуміється їх вільне поперечне переміщення):
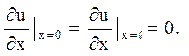 (4.7)
(4.7)
Необхідно помітити, що умови (4.7) є окремим випадком умов (4.6),
виходячи з них при ![]()
![]() . Умови (4.7) можна пояснити геометрично: для
вільного кінця, наприклад
. Умови (4.7) можна пояснити геометрично: для
вільного кінця, наприклад ![]() дотична до графіка функція
дотична до графіка функція ![]() паралель осі x у будь-який момент часу t,
тобто
паралель осі x у будь-який момент часу t,
тобто 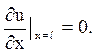 Якщо зовнішні сили відсутні, то в правій
частині рівняння (4.1) функція
Якщо зовнішні сили відсутні, то в правій
частині рівняння (4.1) функція ![]() і замість неоднорідного рівняння виходить однорідне
(замість вимушених коливань – вільні).
і замість неоднорідного рівняння виходить однорідне
(замість вимушених коливань – вільні).
Крайові умови типу (4.3) і (4.7) називають однорідними, а умови типу
(4.4), (4.5) і (4.6) – неоднорідними. Початкові умови (4.2) також в окремому
випадку ![]() називаються
однорідними. Очевидно, всяка неоднорідність ускладнює рішення задачі. Проте,
будь-яка неоднорідна задача може бути вирішена у декілька етапів.
називаються
однорідними. Очевидно, всяка неоднорідність ускладнює рішення задачі. Проте,
будь-яка неоднорідна задача може бути вирішена у декілька етапів.
Для розгляду виберемо задачу про вимушені коливання струни із заданим режимом на кінцях:
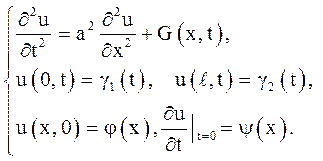 (4.8)
(4.8)
Перший етап. Перш за все слід позбутися неоднорідності в крайових умовах. Для цього необхідно підібрати допоміжну функцію р(x,t), що задовольняє заданим крайовим умовам. Звичайно р(x,t) беруть у вигляді лінійної по x функції:
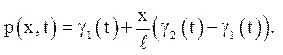 (4.9)
(4.9)
Можна скористатися рівнянням прямої, що проходить через точки ![]() і
і ![]() . Для функції (4.9) граничні умови, очевидно, виконуються.
Тепер вводиться нова невідома функція
. Для функції (4.9) граничні умови, очевидно, виконуються.
Тепер вводиться нова невідома функція ![]() інакше проводиться заміна
інакше проводиться заміна ![]() . Перерахунок других похідних дає:
. Перерахунок других похідних дає:
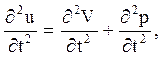
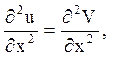 оскільки
оскільки 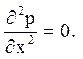
Початкові умови приймають вигляд
![]()
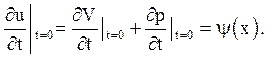
Отже, нова функція ![]() є рішенням наступної задачі
є рішенням наступної задачі
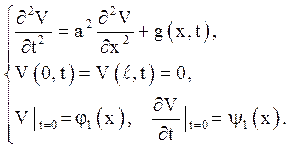 (4.10)
(4.10)
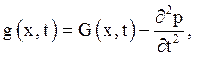
![]()
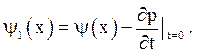
Другий етап полягає в
розбитті даної задачі на дві більш прості задачі. Покладемо ![]() де
де ![]() і
і ![]() служать рішеннями наступних задач
служать рішеннями наступних задач
а) однорідне рівняння, однорідні краєві умови, неоднорідні початкові умови:
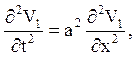
![]() (4.11)
(4.11)
![]()
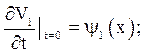
б) неоднорідне рівняння, нульові початкові і краєві умови:
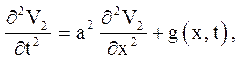
![]() (4.12)
(4.12)
![]()
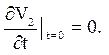
Якщо задачі (4.11) і (4.12) буде вирішений, то, очевидно, сума ![]() буде рішенням задачі (4.10). Задача (4.11)
розв'язується методом Фур’є:
буде рішенням задачі (4.10). Задача (4.11)
розв'язується методом Фур’є:
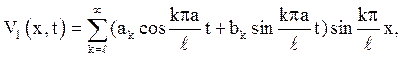 (4.13)
(4.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.