Рівняння математичної фізики: Навчальний посібник, страница 7

Потім розшукуються нетривіальні рішення рівняння, що задовольняють крайовим умовам у вигляді

Повторюючи міркування розділу 3, можна отримати крайову задачу для функції Х(х):

                                         (5.2)

                                            (5.3)

Загальне рішення рівняння (5.2) має вигляд:

Оскільки розшукуються рішення, що задовольняють крайовим умовам (5.3), слід обчислити похідну

і підставити значення х=0:

  откуда 

Після підстановки x=, маємо  звідки   або 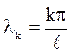  – це власні значення.

Значить, кожному фіксованому значенню k  відповідає рішення 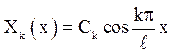 – це власні функції задачі (5.2)-(5.3). Слід помітити, що тут, на відміну від рoзд. 3,   Важливо особливу увагу звернути на значення   якому відповідає власна функція .

Тепер необхідно відшукати функцію . Кожному власному значенню  відповідає функція , визначувана рівняннями

         

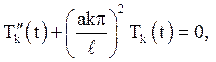
Загальне рішення першого рівняння є лінійна функція:

Загальне рішення другого рівняння має вигляд:

;        

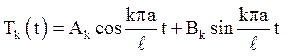Значить, нетривіальні рішення рівняння вільних коливань, що задовольняють крайовим умовам, представляються у вигляді:

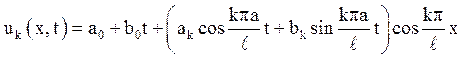
Тут введені нові позначення

            

Залишилося скласти ряд

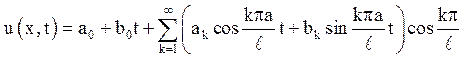         (5.4)

і визначити постійні  і  так, щоб функція  (5.4) задовольняла початковим умовам:

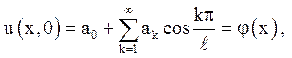
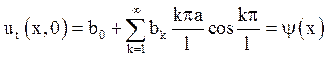                     (5.5)

Вирази (5.5) показують, що  і 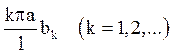  є коефіцієнтами Фур’є розкладання функцій  і  ряд по косинусах на :

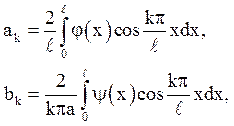                           (5.6)

Коефіцієнти      і     визначаються формулами

        

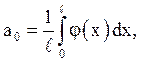
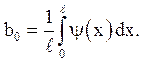
2. Більш загальна задача про вимушені коливання струни із заданими на кінцях силами

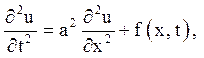
                         (5.7)

      

може бути зведений до вже розглянутим вище за допомогою послідовного застосування трьох етапів (правил) (див. розд. 4).

Згідно правилу 1, вимагається побудувати допоміжну функцію  задовольняючу граничним умовам. В розд. 4, де граничні умови накладалися на саму функцію  ,   була лінійною по x. Тут граничні умови накладаються на похідну  це приводить до думки проінтегрувати лінійну функцію , тобто узяти  у вигляді:

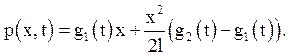                      (5.8)

Легко перевірити, що ця функція задовольняє заданим граничним умовам. Значить, якщо шукати рішення у вигляді суми

то нова невідома функція  є рішення задачі:

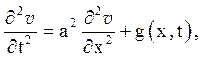
                                          (5.9)

 

де                                 

Згідно правилу 2, слід шукати рішення задачі (5.9) у вигляді

Тут функція  це рішення задачі з неоднорідністю тільки в початкових умовах:

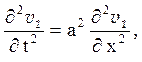
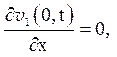
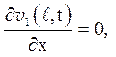                                       (5.10)

 

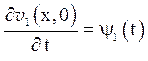
Задача (5.10) співпадає із задачею (5.1), рішення якої отримано методом Фур’є у вигляді ряду (5.4).

Другий доданок  є рішення задачі з неоднорідністю тільки в рівнянні:

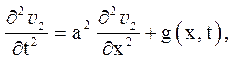                               (5.11)

          

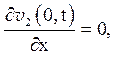
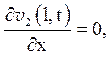
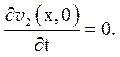
Відповідно до правила 3 рішення задачі (5.11) слід шукати у вигляді ряду по власних функціях задачі (5.1):

.

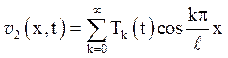Функції  визначаються як рішення задачі Коші для звичайного диференціального рівняння 2-го порядку.

3. Коливання струни із заданим режимом на одному кінці і заданою силою на іншому кінці.

Дана задача має вигляд

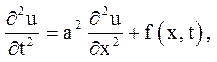
                       (5.12)

 

Спочатку необхідно позбутися неоднорідності в граничних умовах за допомогою правила 1. Як і в розд. 4,  рекомендується шукати у вигляді лінійної по х функції:

з невизначеними коефіцієнтами а, b, с, d. Задовольняючи граничним умовам задачі (5.12):

і прирівнюючи коефіцієнти при  і при , можна отримати:

           

Таким чином, функція

задовольняє граничним умовам задачі (5.12).

В результаті застосування правила 2 намічається підхід до двох задач:

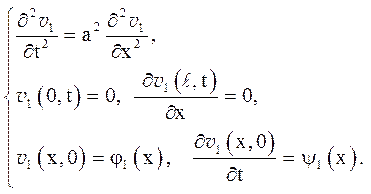              (5.13)

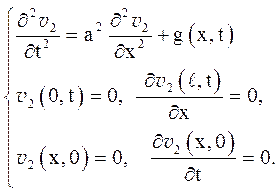                            (5.14)

Рішення задачі (5.13) знаходиться методом Фур’є. Власні функції задачі (5.13) мають вигляд

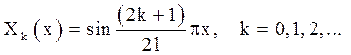
Далі слід поступати відповідно до правила 3, тобто, рішення задачі (5.14) шукати у вигляді ряду

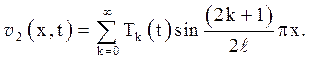
Остаточне рішення представляється у вигляді суми

4. Коливання струни, один кінець якої закріплений пружно, а на іншому задана сила.

Розглядається задача

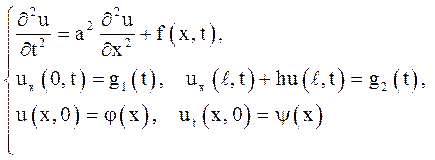       (5.15)

Згідно правилу 1, спочатку будується лінійна по x функція

Тепер необхідно задовольнити граничним умовам задачі (5.15) для визначення невідомих коефіцієнтів a, b, с, d.

Звідси

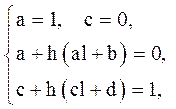
що дає     ,      .

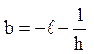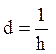Отже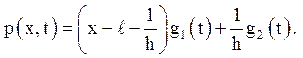         

Далі доцільно діяти за правилами 2 і 3. Тільки слід вказати, що власні функції в даному випадку мають вигляд

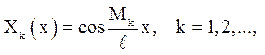
де М_k  –  позитивні корені трансцендентного рівняння

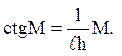                                               (5.16)

Задачі для самостійного розв’язування

На відрізку    для рівняння  вирішити задачі з наступними умовами:

1.    

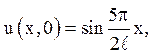
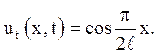
Відповідь:

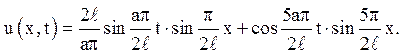
2.    

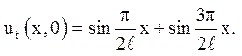
Відповідь:

 

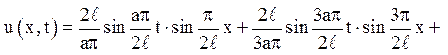
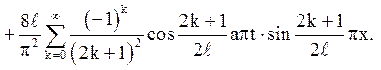
3.    

 Відповідь:

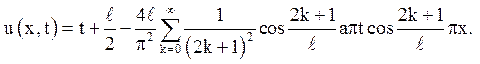
 4.    

Відповідь:

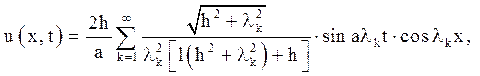
де l_k – позитивні корені рівняння .

5. На відрізку    для рівняння  вирішити задачу з наступними умовами:

      

Відповідь:

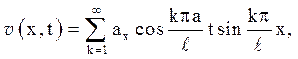
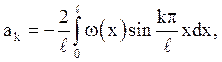
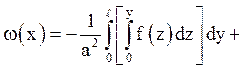
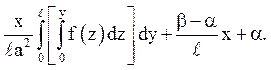
6. Знайти закон вільних коливань струни, розташованої на відрізку  , якщо в початковий момент їй надали форму кривої 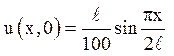 . Потім відпустили без початкової швидкості. Струна закріплена на лівому кінці, а правий може вільно переміщатися так, що дотична в правому кінці весь час залишається горизонтальною.

Відповідь:      

6. БІЛЬШ ПРОСТЕ ПРАВИЛО У ВИПАДКУ
СТАЦІОНАРНИХ ЗОВНІШНІХ СИЛ

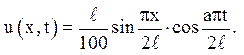
Необхідно пам'ятати, що універсальний метод,  заснований  на  застосуванні правил 1-3, придатний для вирішення будь-якої неоднорідної задачі. Але в універсальності методу - його недолік. В деяких випадках для відшукання функції  можливо використовувати більш прості прийоми, ніж правило 3, рекомендуюче шукати рішення у вигляді ряду по власних функціях.

Пропонується розглянути задачу про вимушені коливання струни з крайовими умовами загального вигляду, зовнішня сила не залежить від часу (стаціонарна).

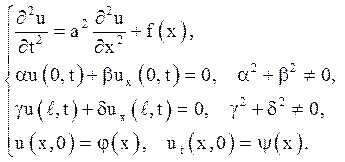             (6.1)

Четвертий етап. (перенесення неоднорідності з рівняння в початкові умови). Рішення задачі (6.1) слід шукати у вигляді:

Хай у(х) є рішення крайової задачі для звичайного диференціального рівняння: