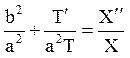
Ліва частина не залежить від x, а права – від t. Рівність можливо лише у тому випадку, коли ці частини постійні
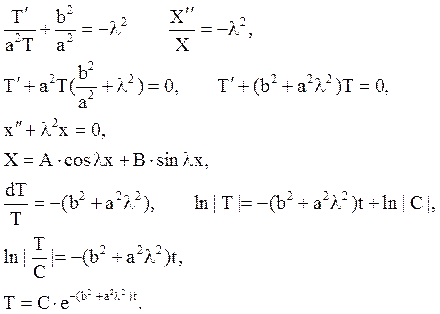
Підставляючи X(x) і T(t) в w(t,x), отримаємо
![]()
Оскільки T(t) ≠ 0, бо було б w(x,t) º 0, то знаходячи похідну х, одержуємо
![]()
Поставляючи сюди х =
0 і х = ![]() , маємо
, маємо ![]()
звідки В = 0
![]() ,
,
звідки sinl =0, ln=pn; n = 0, 1, 2..,
х º 0 и w º 0
Таким чином, Хn(х)= А cos p nx. Враховуючи ln, запишемо
![]()
Таким чином, власні функції задачі Штурма-Ліувілля знайдені
![]()
і рішення нашого рівняння запишеться у вигляді
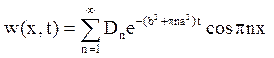
Тут Dn=CnА. Залишилося задовольнити початковим умовам:
w(x,0)= f(x) – v(x)= - 5,
w(x,0)= -5 =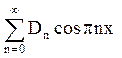 .
.
Розкладаючи Р(х) = -5 на відрізку 0,1 в ряд по косинусах (тобто продовжуючи її парним чином), маємо
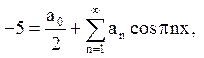
де 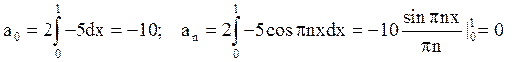
таким чином, Dn=an=0 для n³ 1, і рішення має вид w(x, t)=D0e![]() оскільки
оскільки 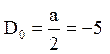 .
.
Таким чином, рішенням початкової задачі є функція
u(x,t)=v(x)+w(x,t)=![]()
Перевірка:
ut=5b2![]() ; uxx = 0; -b2u=
-b2+5b2
; uxx = 0; -b2u=
-b2+5b2![]()
ut=a2uxx - b2u + b2;
5b2![]() = 0 – 5 b2(1-5
= 0 – 5 b2(1-5![]() ) + b2,
) + b2,
тобто рішення знайдено вірно, ця функція задовольняє також початковим і крайовим умовам.
1. Знайти рішення рівняння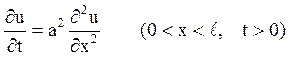 , яке задовольняє умовам u(0,t)= u(l, t) = 0, t > 0
, яке задовольняє умовам u(0,t)= u(l, t) = 0, t > 0
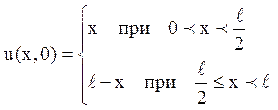
Відповідь:
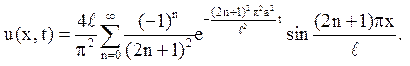
2. Даний тонкий
однорідний ізольований стрижень завдовжки l, початкова температура якого 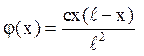 . Кінці стрижня підтримуються при температурі,
рівній нулю. Визначити температуру стрижня у момент часу t > 0.
. Кінці стрижня підтримуються при температурі,
рівній нулю. Визначити температуру стрижня у момент часу t > 0.
Відповідь:
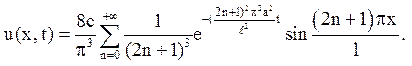
3. Даний тонкий однорідний стрижень завдовжки l, бічна поверхня якого теплоізольована. Початкова температура стрижня відома. На обох кінцях стрижня (х = 0 і х =l) відбувається теплообмін з навколишнім середовищем, температура якого вважається рівною нулю. Визначити температуру стрижня у момент часу t > 0.
Відповідь:
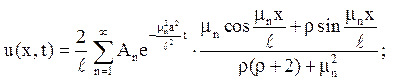
де 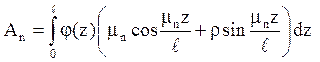 ;
;
m1, m2, m3…. позитивні корені рівняння
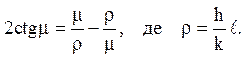
Вказівка. Крайові умови:
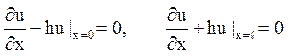 .
.
4. Вирішити задачу про охолодження однорідного стрижня з теплоізолйованою бічною поверхнею, якщо його початкова температура u(x,0)=j(x).
Один кінець теплоізолйований, а інший підтримується при постійній температурі u0.
Відповідь:
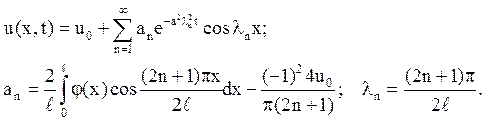
Вказівка. Задача приводиться до інтегрування рівняння 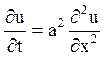 за умов
за умов 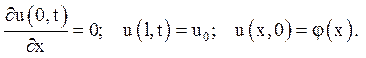 Рішення
слід шукати у вигляді u(x,t)=u0+v(x,t), де v(x,t) - невідома функція.
Рішення
слід шукати у вигляді u(x,t)=u0+v(x,t), де v(x,t) - невідома функція.
5. Знайти стаціонарне розподілення
температури всередині нескінченного циліндру радіусу ![]() ,
якщо на лівій половині поверхні циліндру (0≤φ<π) підтримується температура
–Т, а на правій половині (-π≤φ<0) – температура Т. Вирахувати температуру в
точці
,
якщо на лівій половині поверхні циліндру (0≤φ<π) підтримується температура
–Т, а на правій половині (-π≤φ<0) – температура Т. Вирахувати температуру в
точці
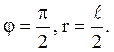
Відповідь:
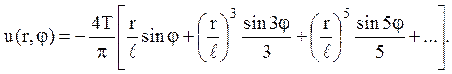
Зокрема, в точці 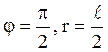 отримуємо
отримуємо
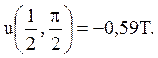
6. Всередині нескінченного колового циліндра
радіусу l відбувається рух нестискаємої рідини. Вважаючи рух установленим, потенційним
і плоскопаралельним, знайти закон руху, якщо проекція швидкості ![]() на зовнішню нормаль циліндра в
кожній точці на поверхні циліндра задається формулою:
на зовнішню нормаль циліндра в
кожній точці на поверхні циліндра задається формулою:
проекція ![]() на
на
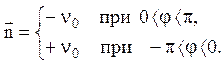
Відповідь: 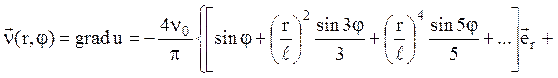
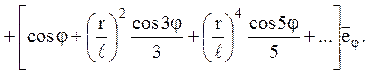
7. Знайти закон охолодження нескінченного циліндра радіусу l, якщо в початковий момент температура всіх його внутрішніх точок дорівнює А , а на його поверхні підтримується постійна температура 0°. Знайти перший член розкладу в ряд.
Відповідь:
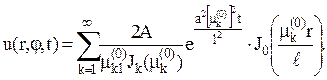
Зокрема, перший член ряду ![]()
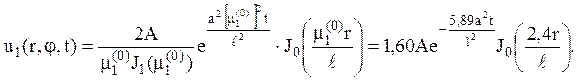
8. Знайти функцію , гармонічну всередині кола радіусу R з центром на початку координат і таку , що:
1)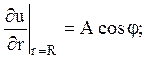 2)
2) 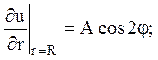 3)
3) 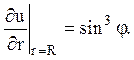
Відповідь:
1) Ar cosj + C; 2) 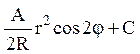 ; 3)
; 3) 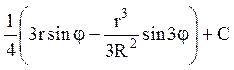 .
.
9. Знайти стаціонарне розподілення
температури ![]() всередині нескінченного циліндра
радіусу R, якщо на його поверхні
підтримується температура
всередині нескінченного циліндра
радіусу R, якщо на його поверхні
підтримується температура ![]()
Відповідь: 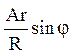 .
.
10.Знайти функцію, гармонічну в колі 1<r<2 і таку, що ![]()
![]()
1) ![]()
![]()
2) ![]()
![]()
Відповідь:
1) 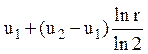 ; 2)
; 2) 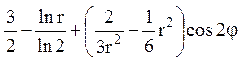 .
.
11. Дослідити радіальний розподіл теплоти в
нескінченному круговому циліндрі радіуса ![]() ,
бічна поверхня якого підтримується при сталій температурі
,
бічна поверхня якого підтримується при сталій температурі ![]() . Початкова температура всередині циліндра
дорівнює нулю.
. Початкова температура всередині циліндра
дорівнює нулю.
Відповідь :
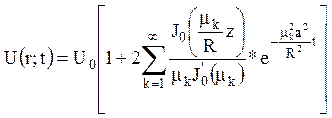 .
.
12. Початкова
температура тонкого однорідного стрижня довжиною ![]() дорівнює
нулю. На кінці
дорівнює
нулю. На кінці ![]() температура підвищується з
часом
температура підвищується з
часом ![]() . На кінці
. На кінці ![]() підтримується
нульова температура. Знайти розподіл температури вздовж стрижня
підтримується
нульова температура. Знайти розподіл температури вздовж стрижня ![]() .
.
Відповідь :
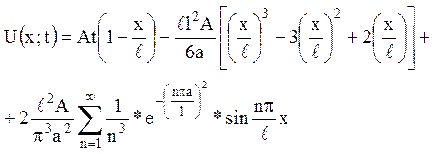
13. Знайти розподілення температури в стрижні, кінці якого підтримуються при заданих температурах, :
![]() ,
, ![]() ,
,
![]() .
.
Початкова температура ![]() .
.
Відповідь :
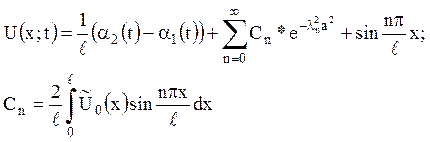 .
.
14. Знайти розв¢язок одномірного
хвильового рівняння 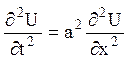 при 0<x<
при 0<x<![]() , t>0,
, t>0,
Який дозволяє крайові
![]()
![]() при
t>0
при
t>0
І початкові умови
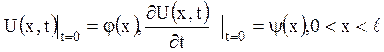
Відповідь:
![]()
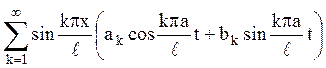
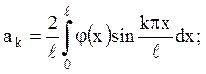
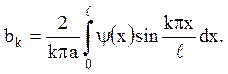
15. Знайти рішення ![]() одномірного
рівняння теплопровідності
одномірного
рівняння теплопровідності
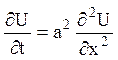 при 0<x<
при 0<x<![]() , t>0,
, t>0,
Який задовольняє крайові
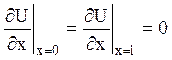 при
при ![]() >0
>0
І початкову умови
![]() при 0<x<l.
при 0<x<l.
Відповідь:
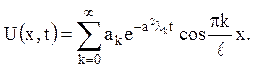
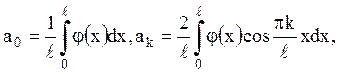 k=1,2,…
k=1,2,…
16. Знайти розв¢язок ![]() одномірного рівняння теплопровідності
одномірного рівняння теплопровідності
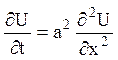 при 0<x<
при 0<x<![]() , t>0,
, t>0,
Який задовольняє крайові умови
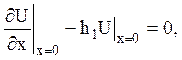
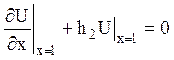 при t>0
при t>0
І початкову умову
![]() при 0<x<l.
при 0<x<l.
Відповідь:
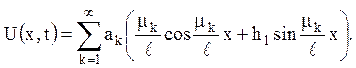
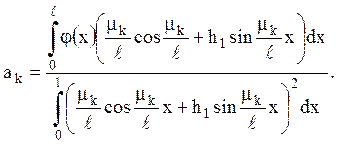
17. Визначити стаціонарний розподіл
температури всередині твердого тіла, яке має форму обмеженого циліндра, якщо до
нижньої основи z=0 підведено сталий теповий потік q, бічна поверхня ![]() і верхня основа
і верхня основа ![]() підтримуються при нульовій
температурі.
підтримуються при нульовій
температурі.
Відповідь: 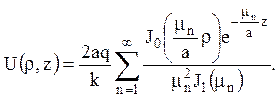
Застосування методу Фур’є для рівнянь еліптичного типу розглянемо на конкретних прикладах.
Приклад 1. Знайти рішення рівняння Лапласа
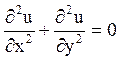
в прямокутнику D: 0 £ x £ а, 0 £ у £ b, на контурі приймаючи задані значення:
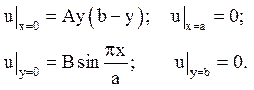
Шукаємо рішення у вигляді
u(x,y)= u1(x,y)+ u2(x,y),
де функція u1(x,y) є рішення задачі
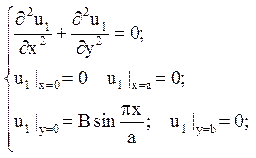
а функція u2(x,y) – рішення задачі
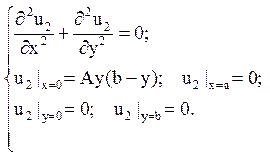
Звертаємо увагу на те, що для функції u1(x,y) однорідними є крайові умови по х, а для функції u2(x,y) однорідними є крайові умови по у.
Шукаємо функцію u1(x,y) у вигляді
u1(x,y)= X(x) У(y)
Після підставки в рівняння і розділення змінних одержуємо
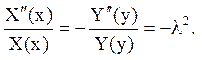
Для функції Х(х) одержуємо задачу Штурма-Ліувілля: знайти нетривіальні рішення крайової задачі
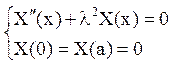
і значення l, при яких ці рішення існують. Одержуємо
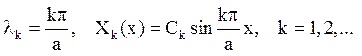
Для визначення функцій Yk(y), відповідних власним значенням lk, маємо рівняння
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.