Отже, дане рівняння
належить до параболічного типу при ![]() та при
та при ![]() (до початку координат рівняння вироджується);
до гіперболічного типу при
(до початку координат рівняння вироджується);
до гіперболічного типу при ![]() .
.
Складаємо рівняння характеристик:
![]()
або ![]()
Одержуємо два диференціальні рівняння:
xdy + ydx=0 і xdy - ydx=0;
розділяючи змінні і інтегруючи, маємо
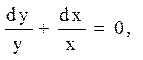 тобто lny + lnx = lnC1
тобто lny + lnx = lnC1
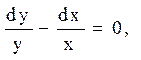 тобто lny - lnx = lnC2
тобто lny - lnx = lnC2
Після потенціювання знаходимо xy = C1 і у/x = C2 – рівняння двох сімейств дійсних характеристик.
Тепер слід ввести нові змінні
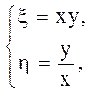 (1.8)
(1.8)
і обчислити похідні
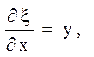
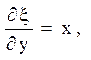
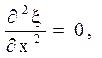
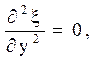
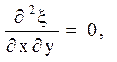
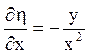
![]()
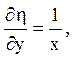
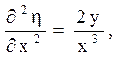
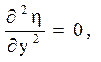
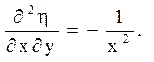
Далі можна скористатися формулами (1.7):
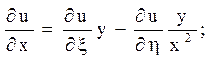
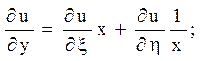
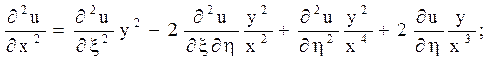
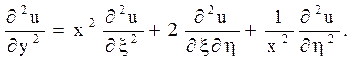
Після підстановки знайдених похідних в задане рівняння
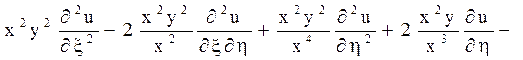
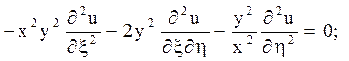
і підрахунку коефіцієнтів
при 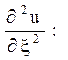 x2y2 – x2y2 = 0;
x2y2 – x2y2 = 0;
при 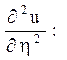
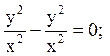
при 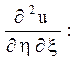 -2y2 – 2y2 = -4y2;
-2y2 – 2y2 = -4y2;
при 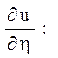
![]()
Рівняння приймає вигляд:
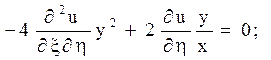
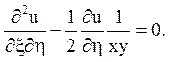
Залишилося виразити через нові змінні xy: ху = x. В нових змінних рівняння має вигляд:
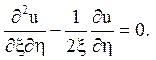
2. Покладемо B2-AC=0. В цьому випадку рівняння (1.5) і (1.6) –
співпадають, і виходить один загальний інтеграл рівняння (1.4) ![]() , тобто сімейство дійсних
характеристик. Вважаючи
, тобто сімейство дійсних
характеристик. Вважаючи ![]() ,
, ![]() де
де ![]() – така
диференційована функція, що якобіан перетворення
– така
диференційована функція, що якобіан перетворення
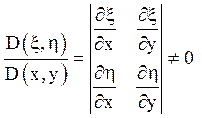 в даній області.
в даній області.
Отже, можна привести рівняння (1.2) до вигляду
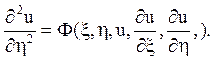
Це канонічний вид рівняння параболічного типу.
Приклад 2. Привести до канонічного вигляду рівняння
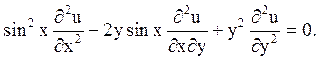
Тут ![]()
![]()
![]()
Отже, дане рівняння належить параболічному типу всюди, де визначена
функція ![]() . Рівняння характеристик має вигляд:
. Рівняння характеристик має вигляд:
![]()
або 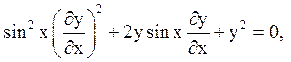 тобто
тобто 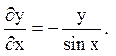
Змінні розділяються: 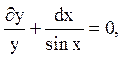 що дає
що дає 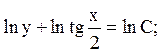 або
або 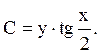 Проведемо заміну змінних:
Проведемо заміну змінних: 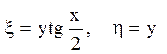 і обчислимо похідні:
і обчислимо похідні:
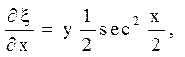
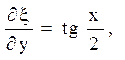
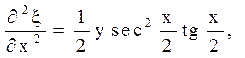
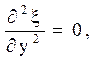
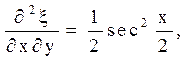
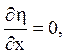
![]()
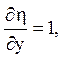
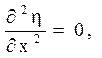
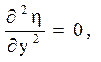
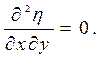
Якобіан дорівнює:
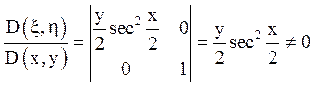
всюди, де y ¹ 0. 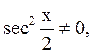
Залишилося перерахувати похідні
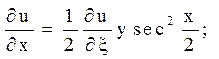
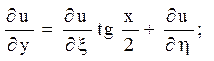
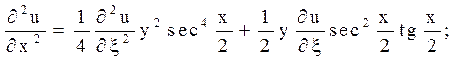
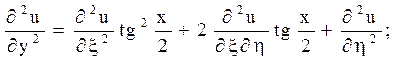
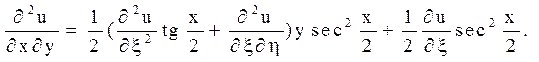
Після підстановки знайдених похідних в задане рівняння
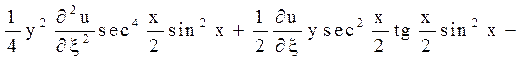
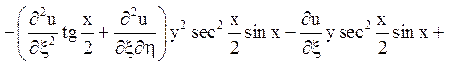
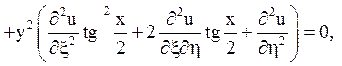
і підрахунку коефіцієнтів
при 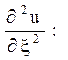
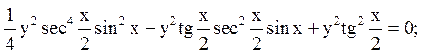
при 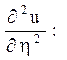 у2;
у2;
при 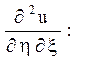
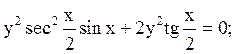
при 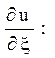
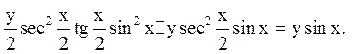
![]()
Рівняння приймає вигляд:
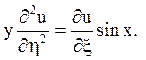
Оскільки 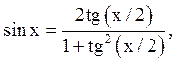
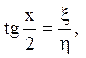 то
то 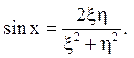
Остаточно одержуємо
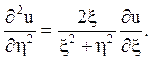
3. Покладемо B2 – АС < 0 . Загальні інтеграли рівнянь (1.5) і (1.6) - комплексно зв'язані, вони визначають два сімейства комплексних характеристик.
Хай загальний інтеграл рівняння (1.5) має вигляд
![]()
де j (x,y) і y (x,y) - речовинні функції.
Тоді, вважаючи, ![]() ,
, ![]() , можна отримати рівняння (1.2) канонічного вигляду:
, можна отримати рівняння (1.2) канонічного вигляду:
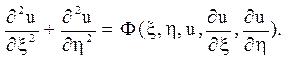
Приклад 3. Привести до канонічного вигляду рівняння
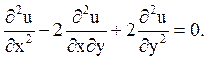
Тут![]()
![]()
![]() ,
, ![]() значить дане рівняння належить еліптичному
типу на всій площині.
значить дане рівняння належить еліптичному
типу на всій площині.
Рівняння характеристик приймає вигляд:
![]()
або
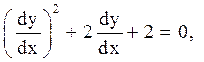 тобто
тобто
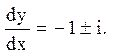
Одержуємо два сімейства уявних характеристик:
![]() и
и ![]()
Проведемо заміну
змінних ![]()
![]() (легко перевірити, що
(легко перевірити, що 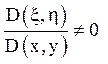 ), після перерахунку приватних похідних і нових
змінних і підстановки в рівняння можна прийти до канонічного вигляду:
), після перерахунку приватних похідних і нових
змінних і підстановки в рівняння можна прийти до канонічного вигляду:
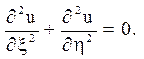
Зауваження. Може виявитися, що в різних частинах області D рівняння (1.2) належить різним типам. Наприклад, для рівняння
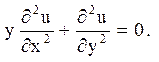
A = y, B = 0, C = 1, значить, ![]() Це рівняння при
Це рівняння при ![]() належить
еліптичному типу, при
належить
еліптичному типу, при ![]() – гіперболічному,
– гіперболічному, ![]() – лінія параболічності. Подібні
рівняння називають рівняннями змішаного типу.
– лінія параболічності. Подібні
рівняння називають рівняннями змішаного типу.
І. Визначити тип диференціального рівняння з частинними похідними:
|
1. 5uxx+2uxy-uyy=0, 4. uxx+2uxy+uyy=0, 7. 3uxy+4uyy=0, 10. uxx+2uxy+uyy=0, |
2. 2uxx+3uxy+4uyy=0, 5. uxx + 6uxy + 13uyy = 0, 8. 3uxx+2uxy+uyy=0, 11. uxx – 6uxy + 18uyy = 0, |
3. uxx + 2uxy+ uyy+ 5ux - 5uy = 0 6. uxx - 2uxy + uyy - 3ux + 3uy = 0, 9. uxx – 4uxy+ 4uyy+ 2ux - 4uy = 0, 12. uxx + 4uxy + 20uyy = 0 . |
ІІ. Звести до канонічного вигляду наступні диференціальні рівняння
1. 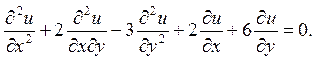
Відповідь: гіперболічного типу на всій площині
![]()
![]()
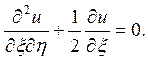
2. 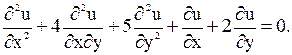
Відповідь: еліптичного типу на всій площині
![]()
![]()
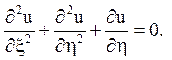
3. 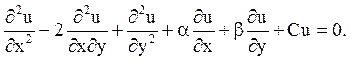
Відповідь: параболічного типу на всій площині
![]()
![]()
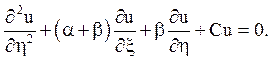
4. 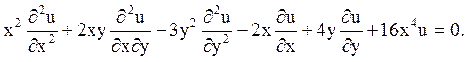
Відповідь: гіперболічного типу на всій площині, окрім осей координат (на початку координат рівняння вироджується)
![]()
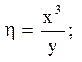
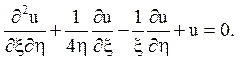
5. 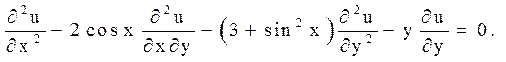
Відповідь: гіперболічного типу на всій площині
![]()
![]()
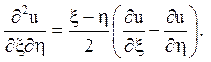
6. 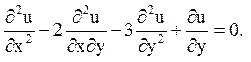
Відповідь: гіперболічного типу на всій площині
![]()
![]()
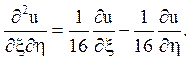
7. 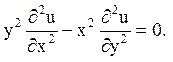
Відповідь: гіперболічного типу у кожному квандранті
![]()
![]()
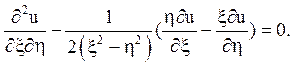
8. 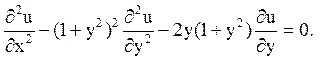
Відповідь: гіперболічного типу на всій площині
![]()
![]()
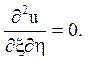
9. 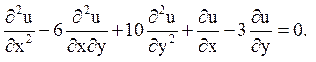
Відповідь: еліптичного типу на всій площині
![]()
![]()
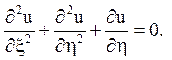
10. 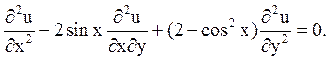
Відповідь: еліптичного типу на всій площині
![]()
![]()
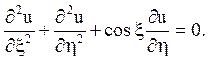
11. 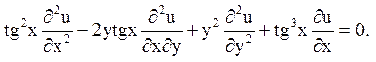
Відповідь: параболічного типу
![]()
![]()
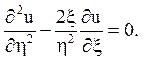
12. 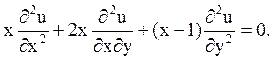
Відповідь: 1) параболічного типу при х = 0; 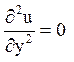 ;
;
2) гіперболічного
типу при х > 0; ![]()
![]()
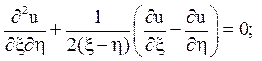
4) еліптичного типу при х <0;
5) ![]()
![]()
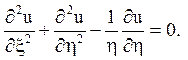
13. 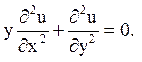
Відповідь: 1) еліптичного типу при y > 0;
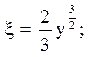
![]()
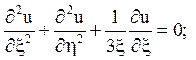
2) гіперболічного типу при y < 0;
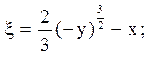
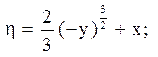
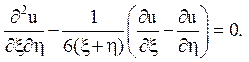
14. 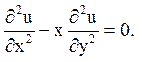
Відповідь: 1) еліптичного типу при x < 0;
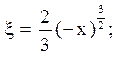
![]()
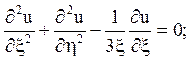
2) гіперболічного типу при x > 0;
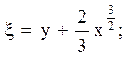
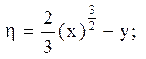
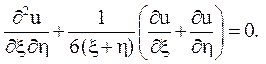
15. 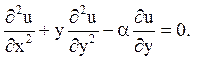
Відповідь: 1) еліптичного
типу при y > 0; ![]()
![]()
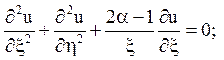
2) гіперболічного типу при
y < 0; ![]()
![]()
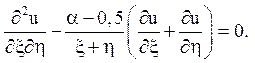
16. 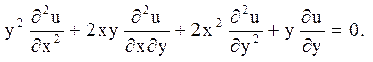
Відповідь: еліптичного типу у кожному квандранті
![]() ,
, ![]() ,
,
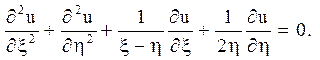
Метод Даламбера, або метод характеристик рішення крайової задачі для рівняння гіперболічного типу покажемо на прикладі вільних коливань нескінченної струни. Розглядаючи вільні коливання, вирішимо однорідне рівняння
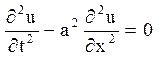 (2.1)
(2.1)
за заданих початкових умов
![]()
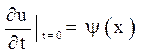 .
(2.2)
.
(2.2)
Спочатку необхідно перетворити рівняння (2.1) до канонічного вигляду.
Рівняння характеристик ![]() розпадається на два рівняння
розпадається на два рівняння ![]() і
і ![]() загальними інтегралами, яких є сімейства прямих
загальними інтегралами, яких є сімейства прямих ![]()
![]()
Потім слід ввести нові змінні ![]()
![]() і
перерахувати похідні:
і
перерахувати похідні:
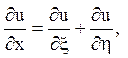
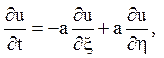
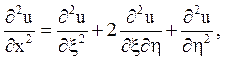
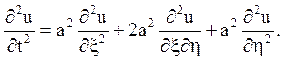
Після підстановки в початкове рівняння (2.I) і приведення подібних
виходить 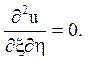 Загальний інтеграл цього рівняння має вигляд
Загальний інтеграл цього рівняння має вигляд
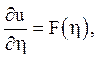 (інтегрування проводиться по x при фіксованому h). Тут
(інтегрування проводиться по x при фіксованому h). Тут ![]() – довільна функція. Повторне інтегрування по h при
фіксованому x дає:
– довільна функція. Повторне інтегрування по h при
фіксованому x дає:
![]()
тут f1 і f2 - довільні функції.
Знайдемо загальне рішення рівняння (2.1) повертаючись до старих змінних:
![]() (2.3)
(2.3)
Слід визначити функції f1 і f2 з початкових умов (2.2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.