Рівняння математичної фізики: Навчальний посібник, страница 11

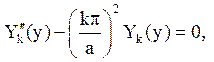
звідки                               

Крайова умова u₁|_y=b= 0 приводить до співвідношення

звідки знаходимо

B_k=

Тоді

,

або, якщо ввести нову постійну  , отримаємо

.

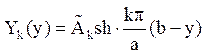Значить, функції  має вигляд

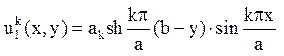
де  a_k =

Залишилося скласти ряд

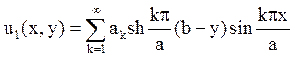
і підібрати коефіцієнти a_k, так, щоб задовольнялася крайова умова

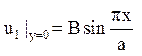
Одержуємо співвідношення

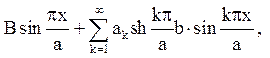
тобто 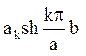 - це коефіцієнти розкладання в ряд Фур’є по синусах на (0, а) функції  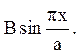Одержуємо

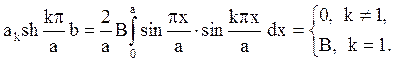
Значить, 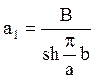, вся решта коефіцієнтів дорівнює нулю, тобто

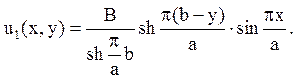
Функцію u₂(x,y)  також шукаємо у вигляді 

u₂(x,y)= X(x)∙Y(y)

Але тут задачу Штурма_- Лівувіля треба отримати для функції Y(y) (однорідність по у крайових умов), тому змінні розділимо таким чином:

.

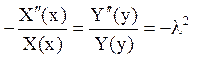Рішенням задачі

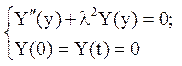
є функції 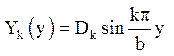, власні значення 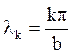, k = 1, 2… .

Для функцій Х_k(х) одержуємо рівняння

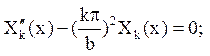
загальне рішення якого

Умова u₂|_x=a= 0 приводить до співвідношення

звідки знаходимо        .

Тоді

або після введення нової постійної  отримаємо

.

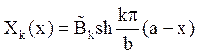Значить, функції  має вигляд

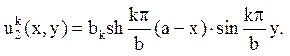
тут . Складемо ряд

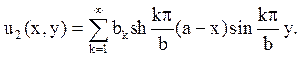
Визначаючи коефіцієнти b_k так, щоб задовольнити крайовій умові  u₂|_х=0 = Ay(b - y), одержуємо

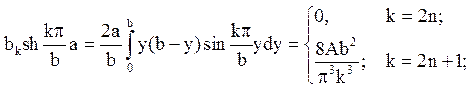
тобто

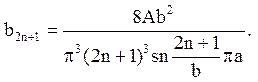
Значить

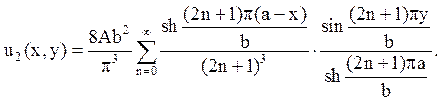
Відповідь:

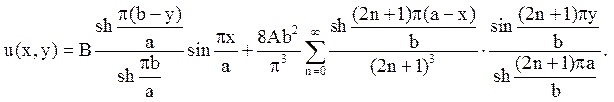
Приклад 2. Знайти гармонійну функцію усередині кільця  ,  задовольняючу крайовим умовам

u|_r=1=0;    u|_r=2=2Asinj.

Рівняння Лапласа в полярних координатах має вигляд

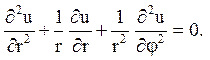
Шукаємо рішення у вигляді u (r, j) = R(r) Ф(j). Підставимо в рівняння і розділимо змінні

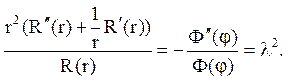
Вирішуємо рівняння Ф"(j)+l²×Ф(j) = 0. Загальне рішення      Ф = Acoslj+ +Bsinlj. Для однозначності функції u(r,j), щоб         u(r,j) = u(r,j+2p),  тоді Ф(j)=Ф(j+2p), а це можливо тільки при l = n, n = 1, 2, 3,… (n береться тільки позитивні, оскільки знак «-» можна віднести до константи).

Отже, Ф_n(j)=A_ncosnj +B_nsinnj. При l = 0 отримаємо рівняння , рішенням якого є лінійна функція

Ф₀(j) = В₀j  + А₀.

Для цього випадку умова Ф(j)=Ф(j+2p) виконуватиметься, якщо В₀ = 0. Отже, Ф₀ = А_0.

Для визначення функцій R_n(r)  одержуємо рівняння Ейлера

Розшукуючи рішення цього рівняння у вигляді R_n(r) = r^a, приходимо до характеристичного рівняння a²-n² =0, корені якого a = ±n. Значить, загальне рішення рівняння (при n¹0) має вигляд

R_n(r)= С_nr^-n + D_nrⁿ.

У разі n= 0 рівняння приймає вигляд

звідки

 

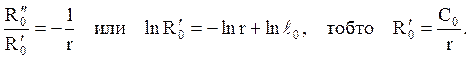
Остаточно R₀(r)= С₀lnr + D₀. Значить, функції  u_n(r,j)  мають вигляд

u₀(r,j) = a₀lnr + b₀       (тут  a₀=C₀A₀, b₀= D₀A₀),

(тут

Складемо ряд

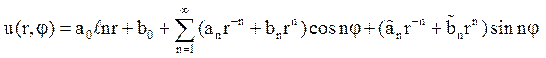
і підберемо коефіцієнти так, щоб задовольнити крайовим умовам.

Вважаємо r = 1:

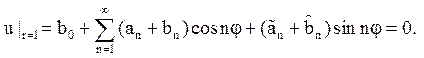
Звідси

 b₀ = 0,   a_n + b_n= 0,       n = 1, 2 .              (1)

При  r = 2

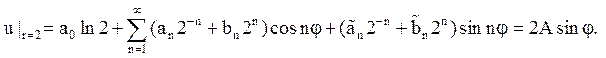
Для визначення коефіцієнтів а₀, a_n, b_n,   треба розкласти ряд Фурье функцію 2Asinj на  (-p,p). Одержуємо

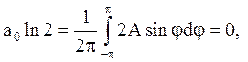    тобто а = 0,

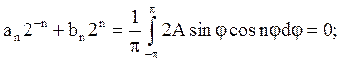                           (2)

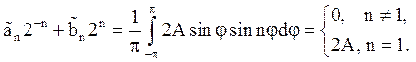
Розглянемо випадок n = 1. Співвідношення (1) приводять до системи:

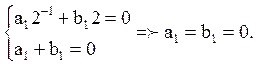
Оскільки визначник цієї однорідної системи відрізнений від нуля, то тривіальне рішення   a₁ = 0,  b₁ = 0 є єдиним. З рівняння (2) одержуємо:

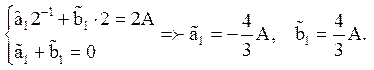
Для випадку  n ¹ 1 маємо дві однорідні системи з відмінними від нуля визначниками:

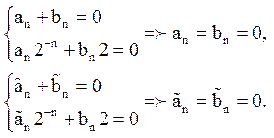
Значить, з нескінченного ряду залишається тільки складове, відповідне n = 1

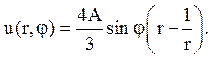
Тут можна перетворити різницю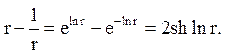 

Відповідь:         .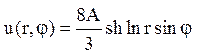

Приклад 3.   Знайти гармонійну функцію усередині кругового сектора  0 ≤ r ≤ R, 0 £ j £ b, задовольняючу на межі умовам:

u(r, 0)= u(r, b) = 0;     u(R, j) = Aj.

Як і в попередній задачі, рішення рівняння Лапласа (в полярних координатах) шукатимемо у вигляді

u(r,j) = R(r)Ф(j).

Функція Ф(j), є рішенням рівняння Ф"(j)+l²Ф(j) = 0, має вигляд

Ф(j) = Фcoslj + Bsinlj

З умов u(r,0)=u(r,b) = 0  випливає, що Ф(0) = Ф(b) = 0. Тоді А = 0 і Bsinlb = 0, але оскільки  В ¹ 0 ( розшукується  нетривіальне рішення), то sin lb = 0, тобто 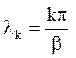 – власні значення і 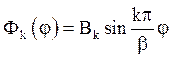- власні функції, k = 1, 2, … .

Функції R_n(r), що задовольняють рівнянню Ейлера

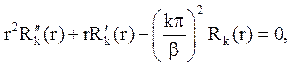
відповідно до коренів характеристичного рівняння мають вигляд

R_k(r)= C_k+

Через обмеженість рішення при  r ®0 слід покласти C_к = 0. Значить, функції u_k(r,j) мають вигляд

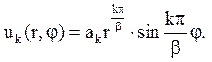
Тут a_k=B_kD_k..

Далі діємо по стандартній схемі. Складаємо ряд

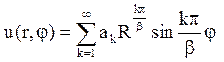
і підбираємо коефіцієнти а_к так, щоб задовольнити умові  u(R,j) = Аj:

.

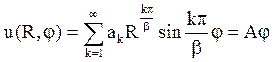Залишилося розкласти функцію  Аj в ряд Фур’є по синусах на [0,b].

Так  

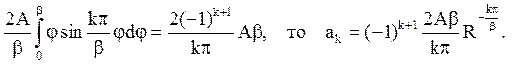
Відповідь:

 

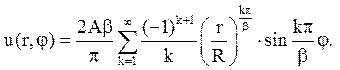
Приклад 4. Знайти стаціонарний розподіл тепла в паралелепіпеді  0£ х £ с,   0 £ g £ b,   0 £ z £ с.  Температура на межі  рівна 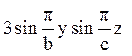, на решті граней температура рівна нулю.

Рішення u(x, у, z)   рівняння Лапласа

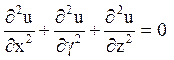                                         (1)

з крайовими умовами

u(0, у, z) = u(x, 0, z) = u(x, у, 0)= 0

u(x, b, z) = u(x, у, з) = 0                                          (2)

u(с, у, z) =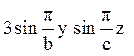

шукатимемо у вигляді

 u(x, у z)=X(x) V(у, z)                                           (3)

Це рішення підказують крайові умови.

Підставимо функцію u(x, у, z) в рівняння (1):

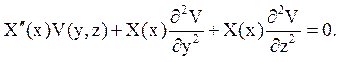
Змінні розділяються:

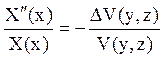                                    (4)

Тут

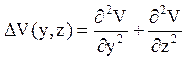
Крайові умови по х дають

u(0, у, z) = X(0)V(у, z)= 0      = >   X(0) = 0;

u(с, u, z) =  X(c)V(у, z) =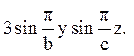

Значить, можемо прийняти  х(с)= 3,  а

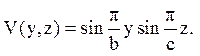                                    (5)

Функція (5) задовольняє нульовим крайовим умовам, тобто V(0,z)= V(b,z)= V(у,0)= V(у, с)= 0. Зверніть увагу на те, що для функції Х(х) ми не отримали задачу Штурма-Ліувілля ( про власні значення і власні функції).

 В співвідношенні (4) ліва частина залежить тільки від х, а права тільки від у, z. Рівність цих частин можливо лише при умові

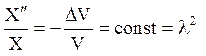                                   (6)

Розглянемо рівняння

DV + l²V = 0                                                   (7)

рішення якого  V(у,z) нам відомо, воно визначається формулою (5). Помітимо, що тільки при позитивних значеннях константи, що фігурує в співвідношенні (6), рівняння (7) може мати рішення  вигляду (5). Знайдемо значення l, при яких  рівняння (7) задовольняється функцією (5).

Обчислимо похідні;

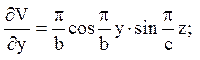
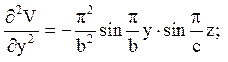
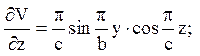
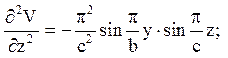
і підставимо їх в рівняння (7)

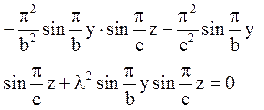
Звідси одержуємо

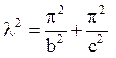   або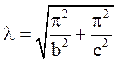  

Залишилося знайти функцію Х(х), яка задовольняє  рівнянню