Автоматизация технологических процессов отрасли, страница 14

Компенсация влияния перекрестных связей

При отсутствии в объекте перекрестных связей двухконтурную систему можно рассматривать как две одноконтурных независимо работающих системы, разделив объект на два. Но если в объекте существуют перекрест-ные связи, что встречается довольно часто, то простейшая схема с независи-мо работающими регуляторами не дает хороших результатов по динамике. Примером наличия перекрестных связей могут послужить концентрация и уровень красильного раствора в плюсовке, влияющие друг на друга (доливая воду – изменяем концентрацию, доливая подкрепляющий раствор – изменяем уровень). Тогда возникает задача в компенсации перекрестных связей.

Для компенсации влияния перекрестных связей в систему вводятся до-полнительные контуры с корректирующими звеньями (КЗ). В зависимости от подключения корректирующих звеньев компенсация перекрестных связей бывает статическая и динамическая.

Статическая компенсация перекрестных связей

Пример статической компенсации приведен на рис. 65:

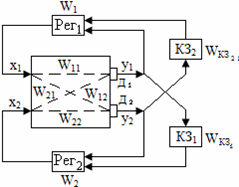
Рис. 65. Схема статической компенсации перекрестных связей

Корректирующие звенья здесь подключаются к выходу датчика, что является недостатком данной схемы, т.к. датчик нагружается двумя потреби-телями и может давать погрешности.

При 2τ>τ1 – получим звено с запаздыванием.

При 2τ<τ1 – получим звено с опережением.

При 2τ=τ1 – получим звено первого порядка без запаздывания.

Во всех трех случаях имеем апериодическое звено с введением произ-водной. В первом и третьем случаях звено реализуется достаточно просто даже в аналоговом варианте. Во втором случае аналоговая реализация звена затруднительна, но в цифровом регуляторе решается без проблем.

Динамическая компенсация перекрестных связей

Пример динамической компенсации приведен на рис. 66:

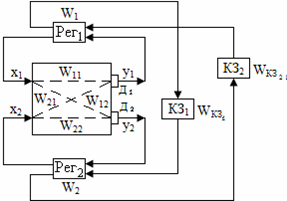
Рис. 66. Схема динамической компенсации перекрестных связей

Корректирующие звенья здесь подключаются к выходу регулятора, а значит, сразу получают достаточно мощный сигнал регулирующего воздействия. Динамическая компенсация перекрестных связей является более удачным вариантом для практического осуществления.

Каскадные САР

Необходимость в каскадных системах возникает, в частности, тогда, когда инерционность контура регулирования соизмерима с периодом изменения возмущающего воздействия f (где f – некая случайная функция времени). Замкнутая САР с действующим на объект возмущением приведена на рис. 67:

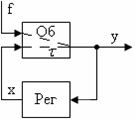
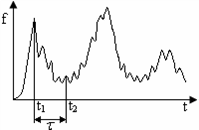
Рис. 67. Замкнутая САР с действующим на объект возмущением

Например, регулятор получил сигнал датчика в момент времени t₁ , но соответствующее регулирующее воздействие (х) поступило в объект в мо-мент t₂=t₁+τ, когда возмущение, вредное влияние которого необходимо ком-пенсировать, существенно изменилось. В этом случае регулятор работает как бы невпопад и может только ухудшить процесс в объекте.

Возникает необходимость в каскадной САР.

Каскадная система предполагает, что кроме основного контура регули-рования строятся вспомогательные (дополнительные) контуры, или каскады, помогающие стабилизировать систему. Рассмотрим некоторые варианты до-полнительных каскадов: