Векторный способ задания движения точки. Координатный способ задания движения точки, страница 9

Задачи для самостоятельного решения
				1.  Полое кольцо радиусом  см вращается в своей плоскости относительно центра О в указанном направлении с постоянным угловым ускорением  (с-1). По кольцу из центра О в указанном направлении движется точка М по уравнению  (см). Вычислить абсолютное ускорение точки М в момент, когда она достигнет положения С.
		2. Прямоугольный треугольник ОАВ вращается с постоянной угловой скоростью  с-1 в своей плоскости вокруг оси, проходящей через вершину О. Точка М движется с постоянным ускорением  см/с2 вдоль стороны треугольника от А к В. Вычислить абсолютные скорость и ускорение точки М в момент времени  с, считая, что в этот момент треугольник ОАВ занимает положение, указанное на чертеже и  см, (начальная скорость точки М равна нулю).
3.  3. По радиусу диска, вращающегося вокруг оси  с угловой скоростью  (рад/с), в направлении от центра диска к его ободу движется точка  согласно уравнению  (см). Радиус  составляет с осью  угол 60°. Вычислить величину абсолютного ускорения точки  в момент  с.
	4.  Прямоугольник  вращается вокруг стороны  с угловой скоростью  (с-1). Вдоль стороны  движется точка  по закону  (м). Даны размеры:  (м), . Вычислить величину абсолютного ускорения точки  в момент времени 1 с.
			5.  Диск вращается с постоянной угловой скоростью  вокруг оси, проходящей через его центр перпендикулярно плоскости диска. По хорде  из ее середины движется точка , согласно уравнению движения  (см). Хорда отстоит от центра диска на расстояние . Вычислить абсолютную скорость и абсолютное ускорение точки .
					6.  Шарик  движется с постоянной скоростью  (м/с) от точки к точке  по хорде диска . Круг вращается замедленно вокруг оси, которая проходит через его центр перпендикулярно плоскости диска. Вычислить абсолютное ускорение шарика, когда он находится на кратчайшем расстоянии от центра диска, равном 30 см. В этот момент угловая скорость диска  (с-1), угловое ускорение  (с-2).
7.  По кольцу радиусом  м из точки О движется точка М согласно уравнению  (м). Кольцо вращается вокруг горизонтальной оси . Вращение кольца задано уравнением  (рад). Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени  с.

4. Плоское движение твердого тела

J

Вспомни теорию

Положение сечения в плоскости  определяется положением отрезка АВ, проведенного в этом сечении (рис. 4.1). Положение сечения  в плоскости можно описать тремя независимыми параметрами – координатами ,  точки А и углом , который отрезок АВ образует с осью . Точку А, выбранную для определения положения сечения , будем называть полюсом.

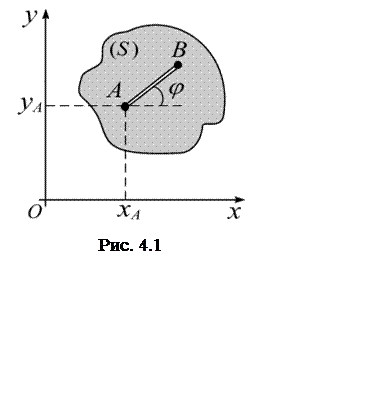При плоском движении твердого тела каждая его точка все время движется в одной и той же плоскости. Следовательно, движение тела в этом случае полностью определяется движением одного из его сечений в к.-л. из параллельных плоскостей, а положение сечения – положением двух точек этого сечения (рис. 4.1).

Уравнения плоскопараллельного движения твердого тела:

,   ,   .

Поскольку координаты , ,  – независимы между собой, плоскопараллельное движение твердого тела можно представить как сумму двух движений: поступательного движения, задаваемого уравнениями , , и вращательного движения тела вокруг полюса А, задаваемого уравнением  (рис. 4.1).

Плоское (плоскопараллельное) движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс А, и из вращательного движения тела вокруг этого полюса (рис. 4.2).

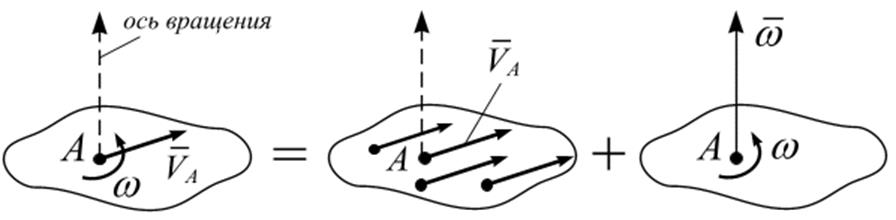
Рис. 4.2

Поступательная составляющая движения:

,

.

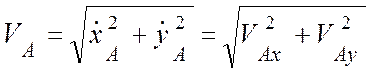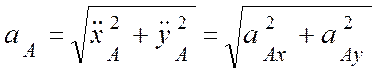Вращательная составляющая движения:

 – уравнение вращения вокруг полюса А;

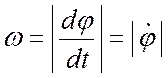 – угловая скорость тела;

 – угловое ускорение тела.

4.1. Скорость

Скорость любой точки тела (например, точки В) при его плоском (плоскопараллельном) движении геометрически складывается из скорости полюса и скорости точки В в её вращении вместе с телом вокруг полюса А:

.

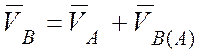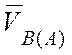В полученном равенстве  – скорость полюса,  – скорость точки В, которую она получает при вращении тела вокруг полюса А:

,   .

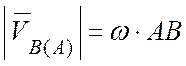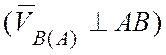Задача 4.1. Диск радиусом R катится без скольжения по линейному рельсу. Центр С диска движется согласно уравнению . Вычислить скорости точек обода диска Р, М, , N, расположенных, как показано на

рис. 4.3.

Решение. Получим уравнения движения диска. Имеем (рис. 4.3, а):

,   ,   .

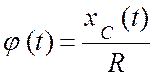а		б
Рис. 4.3

За полюс выберем точку . Вычислим скорость полюса и угловую скорость вращения диска вокруг полюса  Имеем:

,   ,

;   .

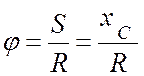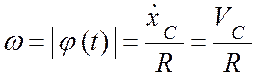Применим к точке Р колеса теорему о скоростях при плоском движении:

.

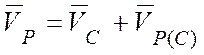Отметим, что ,  .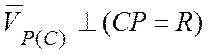

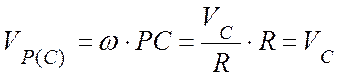Так как векторы  и 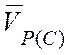 лежат на одной прямой (рис. 4.3, б), имеем:

.

Отметим, что скорости точек, лежащих на ободе диска, по модулю равны между собой, т.к. лежат на одном расстоянии от полюса:

.

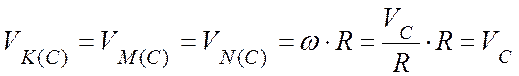Вычислим скорость точки  (рис. 4.3, б):

,

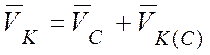здесь 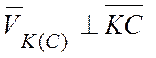          , и :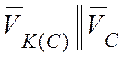

.

Вычислим скорость точки М:

здесь           , :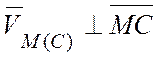

.

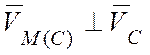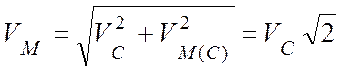Направление скорости находим построением параллелограмма

(рис. 4.3, б). Вычисляем скорость точки N:

Здесь: , :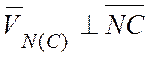

.

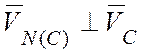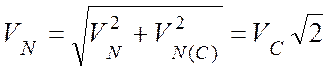Направление векторов скоростей  и  находим построением соответствующих параллелограммов (рис. 4.3, б).

Отметим, что перпендикуляры, проведенные к скоростям в точках М, , N, пересекутся в точке , скорость которой равна нулю.

Ответ:   ;   ;   ;   .

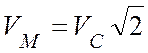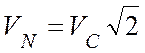J

Вспомни теорию

4.2. Мгновенный центр скоростей

В каждый момент времени при плоском движении тела, если , имеется единственная точка в плоскости его движения, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС). Обозначают ее обычно точкой Р.