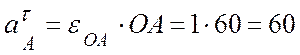 (см/с2)
- касательная составляющая ускорения полюса, направлена
перпендикулярно
(см/с2)
- касательная составляющая ускорения полюса, направлена
перпендикулярно ![]() в сторону углового
ускорения кривошипа ОА -
в сторону углового
ускорения кривошипа ОА - ![]() ;
;
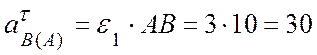 (см/с2)
- ускорения точки В при её вращении относительно
полюса А; вектор
(см/с2)
- ускорения точки В при её вращении относительно
полюса А; вектор 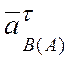 перпендикулярен АВ
и направлен по направлению дуговой стрелки
перпендикулярен АВ
и направлен по направлению дуговой стрелки ![]() ;
;
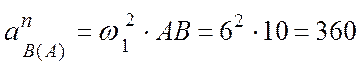 (см/с2),
вектор
(см/с2),
вектор 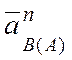 направлен по отрезку АВ от
точки В к точке А.
направлен по отрезку АВ от
точки В к точке А.
Выражение для расчета ускорения точки В записано в векторной форме. Для аналитических вычислений необходимо спроецировать это векторное равенство на две оси координат, тогда теорема примет вид
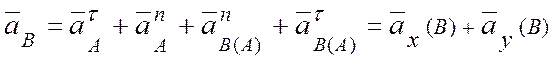 ,
где
,
где
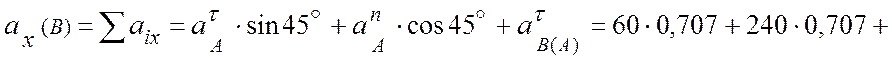
![]() (см/с2);
(см/с2);
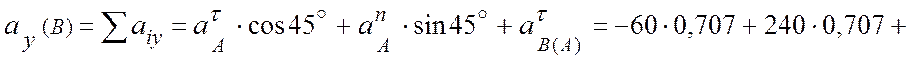
![]() (см/с2).
(см/с2).
Модуль ускорения точки В вычислим по формуле:
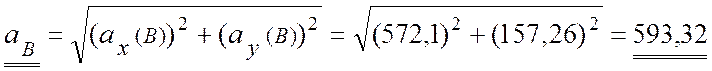 (см/с2).
(см/с2).
Для определения направления вектора полного ускорения
точки В строится параллелограмм на его проекциях ![]() и
и
![]() , диагональ этого параллелограмма и
будет вектором ускорения точки В (рис. 4.11).
, диагональ этого параллелограмма и
будет вектором ускорения точки В (рис. 4.11).
Ответ: ![]() (с-1),
(с-1), ![]() (с-2);
(с-2); ![]() (см/с);
(см/с); ![]() (см/с2).
(см/с2).
Задача 4.4. В кривошипно-шатунном механизме кривошип ОА длиной
40 см вращается
замедленно относительно центра О, с угловой скоростью ![]() с-1 и угловым
ускорением
с-1 и угловым
ускорением ![]() с-2
(рис. 4.12), и приводит в движение шатун АВ длиной 80 см.
с-2
(рис. 4.12), и приводит в движение шатун АВ длиной 80 см.
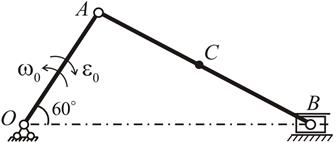
Рис. 4.12
Вычислить:
1. скорость и ускорение точки В ползуна;
2.
скорость и ускорение точки С,
расположенной на шатуне АВ на расстоянии ![]() см.
см.
Решение. В кривошипно-шатунном механизмекривошип ОА вращается относительно центра О, шатун АВ движется плоскопараллельно, ползун В движется поступательно.
Точка А одновременно принадлежит и кривошипу ОА, и шатуну АВ. Рассматривая вращение кривошипа, скорость точки А рассчитываем по формуле
![]() (см/с).
(см/с).
Вектор скорости ![]() перпендикулярен кривошипу ОА
и направлен в сторону угловой скорости кривошипа. Вектор скорости точки В
шатуна направлен вдоль направляющих ползуна, в данном случае - по горизонтали (рис. 4.12).
перпендикулярен кривошипу ОА
и направлен в сторону угловой скорости кривошипа. Вектор скорости точки В
шатуна направлен вдоль направляющих ползуна, в данном случае - по горизонтали (рис. 4.12).
Заменим плоское
движение шатуна АВ мгновенно-вращательным относительно мгновенного
центра скоростей (МЦС). Для нахождения МЦС восстановим перпендикуляры к
построенным векторам скоростей ![]() и
и ![]() , на их пересечении будет находиться
МЦС шатуна - точка Р (рис. 4.13, а).
, на их пересечении будет находиться
МЦС шатуна - точка Р (рис. 4.13, а).
|
а |
|
б |
|
|
Рис. 4.13 |
|||
Направление
мгновенного вращения шатуна АВ вокруг МЦС - ![]() - определяем по
направлению вектора
- определяем по
направлению вектора ![]() .
.
Величина угловой скорости шатуна рассчитывается:
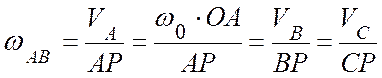 ,
откуда
,
откуда
![]() ,
, ![]() .
.
Если положение кривошипно-шатунного механизма фиксировано и начерчено в масштабе, то расстояния ВР и СР измеряются с чертежа линейкой. В общем случае рассматривают геометрию задачи (рис. 4.13, б).
Для вычисления расстояний АР, ВР, СР рассмотрим треугольники ОАВ и ОРВ:
из ![]() по теореме
синусов:
по теореме
синусов:
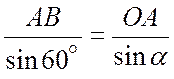
![]()
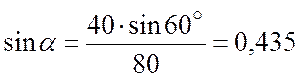 ;
;
![]() ;
; ![]() ,
, ![]() .
.
из ![]() по теореме
синусов:
по теореме
синусов:
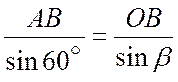 ;
; 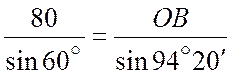 ;
;
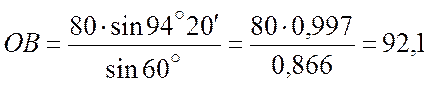 см.
см.
В прямоугольном
треугольнике ![]() угол ОРВ равен
угол ОРВ равен ![]() , поэтому гипотенуза ОР равна
удвоенному произведению катета ОВ, лежащего против угла
, поэтому гипотенуза ОР равна
удвоенному произведению катета ОВ, лежащего против угла ![]() :
:
![]() см,
тогда
см,
тогда ![]() см.
см.
По теореме Пифагора расстояние ВР:
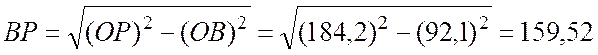 см.
см.
Расстояние СР
определяется из ![]() по теореме косинусов, с
учетом угла
по теореме косинусов, с
учетом угла ![]() :
:
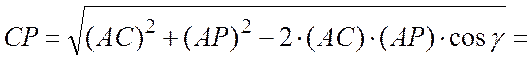
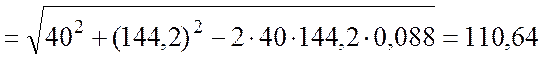 см.
см.
Угловая скорость шатуна АВ, скорости точек В и С вычисляют следующим образом:
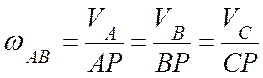 ,
,
откуда 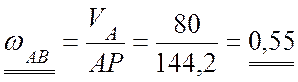 с-1;
с-1;
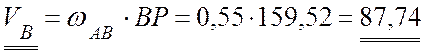 (см/с),
(см/с),
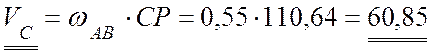 (см/с).
(см/с).
Вектор скорости ![]() перпендикулярен
отрезку РС и направлен в сторону мгновенного вращения шатуна
перпендикулярен
отрезку РС и направлен в сторону мгновенного вращения шатуна ![]() (рис. 4.13, а).
(рис. 4.13, а).
Рассчитываем ускорение точки В ползуна. Принимаем точку А шатуна за полюс, тогда
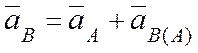 . (а)
. (а)
Здесь (рис. 4.14, а):
![]() - ускорение полюса А:
- ускорение полюса А:
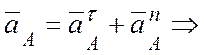
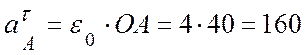 (см/с2) ;
(см/с2) ;
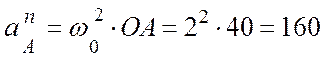 (см/с2).
(см/с2).
![]() - ускорение точки В при ее вращении вокруг полюса А:
- ускорение точки В при ее вращении вокруг полюса А:
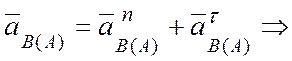
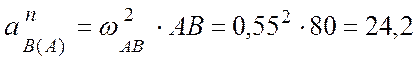 (см/с2),
(см/с2),
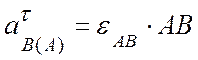 .
.
Вектор 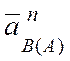 направлен по
шатуну АВ от точки В к точке А; вектор
направлен по
шатуну АВ от точки В к точке А; вектор 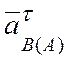 располагаем перпендикулярно шатуну АВ.
располагаем перпендикулярно шатуну АВ.
Сводим вектора ![]() ,
,
![]() ,
, 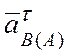 ,
,
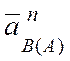 в точку В (рис. 4.14, б).
в точку В (рис. 4.14, б).
|
а |
б |
|
|
|
Рис. 4.14
Ускорение точки В определяется векторным уравнением:
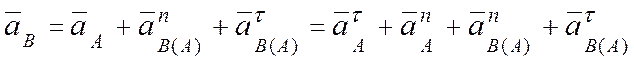 . (б)
. (б)
Таким образом, получили векторное равенство с двумя
неизвестными: ![]() и
и 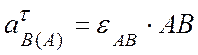 .
.
Вычислить ![]() и
и ![]() можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных
способов.
можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных
способов.
Аналитический способ. Начало декартовой системы координат совместим с точкой
В, ось ![]() с осью ползуна, ось
с осью ползуна, ось ![]() перпендикулярна оси ползуна (рис. 4.14,
б). Вектор ускорения ползуна
перпендикулярна оси ползуна (рис. 4.14,
б). Вектор ускорения ползуна ![]() направлен вдоль
оси
направлен вдоль
оси ![]() , поэтому проекция вектора
, поэтому проекция вектора ![]() на ось
на ось ![]() равна
нулю:
равна
нулю:
- из (б) получаем:
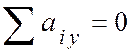 ,
, 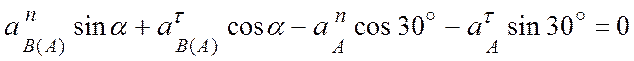 ;
;
![]() ;
;
![]()
![]()
![]()
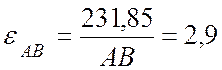 с-2;
с-2;
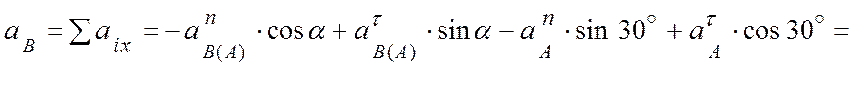
![]() (см/с2);
(см/с2);
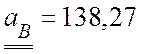 (см/с2).
(см/с2).
Здесь
![]() ,
, ![]() .
.
Вычислим ускорение точки С. Положительный знак 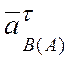 означает, что выбранное на схеме
направление этого вектора совпадает с истинным. Следовательно, угловое
ускорение шатуна
означает, что выбранное на схеме
направление этого вектора совпадает с истинным. Следовательно, угловое
ускорение шатуна ![]() направлено против часовой
стрелки (рис. 4.15, а).
направлено против часовой
стрелки (рис. 4.15, а).
|
а |
б |
|
|
|
Рис. 4.15
Ускорение точки С:
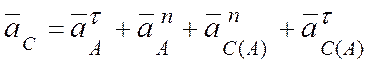 ,
где
,
где
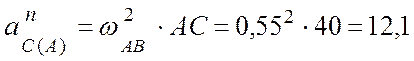 (см/с2),
(см/с2),
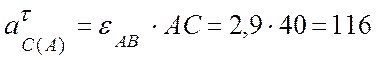 (см/с2).
(см/с2).
Спроецируем записанное векторное равенство на оси ![]() и Сy
и Сy
(рис. 4.14, б):
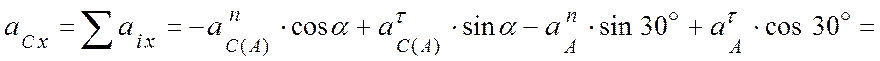
![]() (см/с2);
(см/с2);
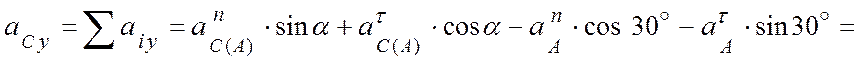
![]() (см/с2).
(см/с2).
Модуль ускорения точки С:
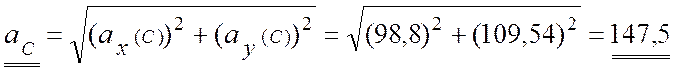 (см/с2).
(см/с2).
Геометрический (графический) способ
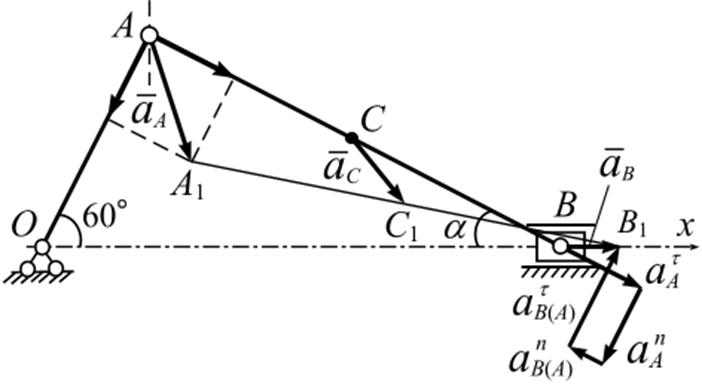
Рис. 4.16
Ускорение ползуна В
можно получить построением многоугольника ускорений (рис. 4.16). Для этого в
принятом масштабе откладываем из точки В ускорение ![]() , далее, перпендикулярно ему,
откладываем касательную составляющую ускорения полюса
, далее, перпендикулярно ему,
откладываем касательную составляющую ускорения полюса ![]() ,
под углом
,
под углом ![]() к горизонту откладываем ускорение
к горизонту откладываем ускорение 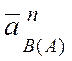 , из его конца проводим пунктирную
прямую, перпендикулярную
, из его конца проводим пунктирную
прямую, перпендикулярную 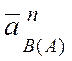 (параллельную
неизвестному ускорению
(параллельную
неизвестному ускорению 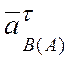 ) до пересечения
с осью
) до пересечения
с осью ![]() , по которой направлен вектор
ускорения ползуна В. Точка пересечения пунктирной прямой и осью
, по которой направлен вектор
ускорения ползуна В. Точка пересечения пунктирной прямой и осью ![]() определяет вектора
определяет вектора 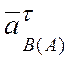 и
и ![]() .
Вектор
.
Вектор ![]() замыкает многоугольник (рис. 4.16).
замыкает многоугольник (рис. 4.16).
Измеряем длины этих векторов и с учетом масштаба получаем соответственно:
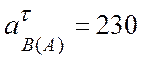 (см/с2),
(см/с2), ![]() (см/с2).
(см/с2).
Для вычисления ускорения точки С
– середины шатуна АВ – соединим концы ускорений точек А и В
(рис. 4.16) отрезком ![]() , разделим его пополам
точкой
, разделим его пополам
точкой ![]() и, соединив точки С и
и, соединив точки С и ![]() , получим вектор ускорения середины
шатуна
, получим вектор ускорения середины
шатуна ![]() . Замерив его с учетом масштаба,
получим
. Замерив его с учетом масштаба,
получим ![]() (см/с2).
(см/с2).
Ответ: ![]() с-1,
с-1,
![]() с-2;
с-2; ![]() (см/с),
(см/с), ![]() (см/с);
(см/с);
![]() (см/с2),
(см/с2),
![]() (см/с2).
(см/с2).
Задача 4.5.
Вычислить аналитически и графически ускорение шарнира В В шарнирного
параллелограмма в его данном положении (рис. 4.17 а), если кривошип ![]() см вращается равномерно
относительно центра О с угловой скоростью
см вращается равномерно
относительно центра О с угловой скоростью ![]() с-1; длины
звеньев
с-1; длины
звеньев ![]() см,
см, ![]() см.
см.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.