Физика \ Физика

Векторный способ задания движения точки. Координатный способ задания движения точки, страница 4

,   .                                                         (с)

Уравнения движения точки (а)-(б) заданы параметрически, т.е. координаты x и y зависят от параметра . Чтобы записать уравнение траектории в декартовой системе координат, из заданных уравнений необходимо исключить параметр .

Из (а) получаем 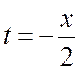, подставляем в (б):

.

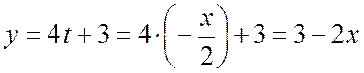Таким образом, получили уравнение траектории

.

1_17

Рис. 1.17

Траекторией движения точки,  распложенной в области , , является отрезок прямой. Движение точки прямолинейное.

Строим траекторию. Для этого достаточно знать координаты двух точек:

при   ,    (см);

при    (см),    (см).

Построим траекторию в выбранном масштабе в плоскости  (рис. 1.17). Функция  убывающая;  - возрастающая. Следовательно, точка из начального положения  начинает движение по прямой вверх. Направление движения отмечено стрелкой на траектории.

При  (с):  (см),  (см);

при  (с):  (см),  (см).

Обозначим указанные положения точками  и , рис. 1.17.

Скорость и ускорения точки  при  с:

 (см/с),    (см/с).

Значение скорости точки не зависит от времени , т.е. точка движется с постоянной скоростью:

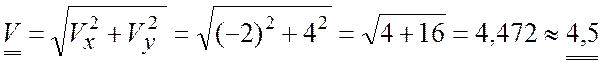 (см/с).

Полученные значения  и  отложим на графике (рис. 1.17) в масштабе. Вектор скорости точки  является диагональю параллелограмма, достроенного на этих значениях с направлением движения точки .

Ускорение точки  при  с:

,   ; .

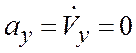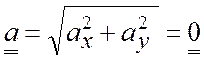Прямолинейное движение точки является равномерным.

При прямолинейном движении нормальное ускорение .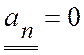

Радиус кривизны траектории:

.

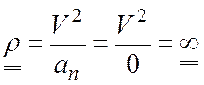Вычислим уравнения движения при  естественном способе :

.

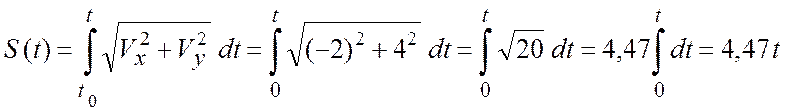Ответ: уравнение траектории в декартовой системе координат: ; скорость точки  (см/с); ускорения точки , , ; радиус кривизны траектории ; .

(!!! Алгоритм решения

Первый тип задач (прямая задача) – заданы уравнения движения точки в плоскости ,  или , требуется вычислить скорость и ускорение точки тела; если движение точки задано координатным способом - то вычислить уравнение траектории в явном виде .

Схема решения:

·  выбирается система координат (или ) и начало координат (та или иная система выбираются исходя из условий задачи так, чтобы дальнейшее решение было по возможности более простым;

·  на основании условий задачи для избранной системы координат составляются уравнения движения точки (если они явно не заданы), т.е. находятся зависимости координат точки от времени – , ;

·  исключая параметр  из уравнений движения, вычисляют траекторию точки как функцию – ;

·  дифференцируя по времени уравнения движения , , или , вычисляют скорость точки;

·  вычисляя вторую производную по времени от , , находят ускорение точки;

·  если движение точки задано естественным способом, т.е. задана траектория движения, радиус кривизны и , вычисляют нормальную и касательную составляющие ускорения;

·  вычисляется полное ускорение точек по модулю и направлению.

Второй тип задач (обратная задача) - заданы проекции ускорения , ; требуется вычислить проекции скорости точки, как функцию времени, т.е.  и вычислить уравнения движения точки в декартовой системе координат, т.е. , .

Схема решения:

·  выбирают систему координат;

·  формулируют начальные условия задачи: ;

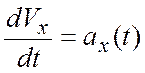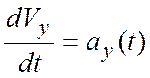·  разделяют переменные в дифференциальных уравнениях и , или 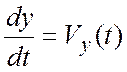,  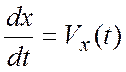и, интегрируя по времени дифференциальные уравнения с разделенными переменными, вычисляют проекции скорости точки , , а также  уравнения движения точки , .

J

Задачи для самостоятельного решения

1. Положение линейки АВ определяется углом  (рад). Вычислить проекцию скорости точки М на ось Ох в момент времени  с, если расстояние  м.

2. Положение кривошипа определяется углом  (рад). Вычислить скорость и ускорение ползуна В в момент времени  с, если  м.

3. Точка движется по прямой с ускорением  (м/с2). Вычислить начальную скорость точки, если через 6 с скорость точки составила 3 м/с.

4.  4. Проекция скорости точки . Вычислить координату х точки в момент времени  с, если в момент времени  координата  м.

5.  Точка движется по прямой с ускорением (м/с2). Вычислить начальную скорость точки, если через 2 с скорость точки составила 6 м/с.

6.  . Движение точки задано уравнениями  и . Вычислить касательное ускорение в момент времени  с.

7.  По заданному уравнению движения точки на произвольно выбранной траектории построить через равные промежутки времени шесть положений точки, определить расстояние  по траектории от начала отсчета до конечного положения точки и пройденный ею путь  за указанный промежуток времени ( и  - в сантиметрах, t - в секундах):

1)  , .

2)  , .

3)  , .

8.  8. По заданным  уравнениям  движения  точки  найти  уравнения  ее траектории в координатной форме и указать на рисунке направление движения: ,   .

1)  ,   .

2)  ,   .

3)  ,   .

9.  Снаряд движется  в  вертикальной  плоскости  согласно уравнениям ,  (t – в секундах, х и у – в метрах). Вычислить: скорость и ускорение в начальный момент; высоту и дальность обстрела; радиус кривизны траектории в наивысшей точке.

10.   Вычислить ускорение точки В в момент времени, когда угол , если длина  см, а закон изменения угла  (рад).

11. Положение кривошипа ОА определяется углом  (рад). Вычислить проекции ускорения ,  точки А в момент времени  с, если длина кривошипа  м.

12. Положение  линейки  АВ  определяется углом  (рад). Вычислить проекции ускорения точки М на оси  и  в момент времени  с, если расстояние  м.

13. Точка  движется  по  прямой  Ох  с  ускорением  .  Вычислить  координату х точки в момент времени  с, если при  скорость  км/ч, и координата .

14. Касательное ускорение точки . Определить момент времени t, когда скорость  точки достигнет 10 м/с, если при  скорость  м/с.

15. Проекции  скорости  точки  во  время  движения  определяются выражениями ,  м/с. Вычислить касательное ускорение в момент времени  с.

16. Даны уравнения движения снаряда

, ,

где  - начальная скорость снаряда,  – угол между  и горизонтальной осью х; g – ускорение силы тяжести. Определить траекторию движения снаряда, высоту Н, дальность L и время Т полета самолета.

17. Кривошип    вращается  с постоянной угловой скоростью . Вычислить скорость середины шатуна точки  кривошипно-ползунного механизма и скорость ползуна В, как функцию от времени, т.е. , , если .

18. Из орудия береговой артиллерии с высоты  м над уровнем моря произведен выстрел под углом  к горизонту, начальная скорость снаряда  м/с. Вычислить, на каком расстоянии от орудия снаряд попадет в цель, находящуюся на уровне моря.

Уравнения движения снаряда в вертикальной плоскости:

,

.
Скачать файл